t分布与t检验的一点理解

最近又遇到了t分布及t检验方面的内容，发现有些地方自己当初没有很明白，就又查了些资料，加深了一下自己的理解，这里也将自己的一些理解记录下来。

1. 理论基础——大数定理与中心极限定理

       在正式介绍t分布前，还是再强调一下数理统计学中的两大基石般的定理：大数定理与中心极限定理，后面会用到。这里我就不以数学公式的方式来说明了，直接说一下两个定理所表达的意思。

• 大数定理。不管是强大数定理还是弱大数定理，都表达着这样一个意思：当样本数量足够大时，这些样本的均值无限接近总体的期望。
• 中心极限定理。不管样本总体服从什么分布，当样本数量足够大时，样本的均值以正态分布的形式围绕总体均值波动。中心极限定理的表达方式可以有多种，我这里只是其中一种。

2. t 统计量

t 统计量是英国化学家、数学家、统计学家 William Sealy Gosset提出的，当年他在爱尔兰的吉尼斯酒厂（这个酒厂还有个很牛的事儿，它的老板编著了现今著名的《吉尼斯世界纪录》）工作时，酒厂禁止其将研究成果公开发表，以免泄露秘密，迫不得已William Sealy Gosset以笔名“The Student”发表研究成果，t统计量及t分布的命名就是源于改笔名。

大麦是酿造啤酒的主要原料，因此酒厂就希望大麦产量越高越好，于是就不断改进大麦种植工艺，此时就需要做试验来比较不同工艺下大麦的产量，但是实际条件不允许（或者为了减轻工作负担）大面积种植麦子来比较工艺的优劣，因此试验田种植是比较合适的方式。比如现在有两片试验田（如下图所示），左边的是采用工艺A种植的麦子，右边的是采用工艺B种植的麦子，两边各种100株麦子。下面我要开始编故事啦。。。

​

现在发现左边麦田中平均每株麦穗上有100粒麦子，右边麦田中平均每株麦穗上有120粒麦子，这说明啥？说明采用工艺B能得到更高的麦子产量对不？咱们外行可能会这么看，但是人家专业的可不轻易这么认为。这是采用小面积的试验田种出的麦子，一个是量少，不足以说明问题（想想咱们的大数定理），另一个是无法保证除工艺区别外其它因素都一样。因此，William Sealy Gosset就想，这20粒麦子的差值能不能说明工艺的优劣问题呢？

William Sealy Gosset知道，每株麦穗上的平均麦子数是有波动的，可能这一次种的麦子平均值是100，下一次就不一定了，可能就是105，也可能是95。那可以这样考虑啊，这20的差值是不是在工艺A下麦子平均产量的正常波动范围内？样本均值的波动可以用样本均值的标准差表示，注意：这里说的是样本均值的标准差，而不是样本的标准差，基于这种想法可以构造这样一个统计量

来评估工艺的优劣，其中是工艺A下每株麦穗上结的麦子数，是工艺B下每株麦穗上结的麦子数，是工艺A下每株麦穗上结的麦子数平均值的标准差。好了，到了这里故事也编得差不多了，t 统计量的由来也差不多就这样了，下面咱们严谨的定义一下 t 统计量，分两种情况，一种是单总体情况，另一种是双总体情况。

• 单总体情况。这种情况下 t 统计量的定义为

式中为样本的均值，为总体的均值，为总体标准差，为样本个数，由于总体标准差无法得知，因此一般用样本标准差来估计总体标准差。从数学上可以证明，若样本个数为，样本均值的标准差（样本均值的波动）等于总体的标准差（总体波动）除以样本个数，我们可以通过大数定理来简单理解一下，当样本个数增大时，样本均值的波动也应该是越小的。总体的标准差是无法获知的，一般用样本标准差来估计。这里着重强调一个概念——标准误，标准误即样本均值的标准差，它对于理解假设检验很重要。

• 双总体的情况。这种情况下t 统计量的定义为

式中为样本1的均值，为样本2的均值，为样本1与样本2均值差值的标准误。这里我不再说明是怎么计算的了，一个原因是比较复杂，需要分几种情况讨论，另一个更主要的原因是如何计算不重要，计算机内置函数会帮我们计算的，重要的是理解 t 统计量是如何提出的以及表示什么意思。

3. t 分布与正态分布

        t 统计量的分布就是 t 分布了，下面我们以单总体时的 t 统计量为例，说明一下 t 分布与正态分布的关系。我们已经知道了样本的均值为，也知道的标准差为，那么依据中心极限定理，样本均值服从均值为，方差为的正态分布，也许你已经发现了，没错，当样本数量足够大时，t 分布无限接近标准的正态分布。

在第一节中也强调了，不管是大数定理还是中心极限定理，都是在样本数量足够大时管用的。在样本数量不是足够大时，尽管t 分布的概率密度曲线和正态分布分布曲线相近，但是还是有所区别，用样本标准差估计总体标准差是一个原因。

​

是t分布的概率密度曲线，这里我不写出的具体公式了，有兴趣的同学可以自行研究，伟大的统计学家们已经研究透测了，并且制作了t分布的概率表。从 t 统计量的定义式看就知道，样本个数的影响非常关键，因此 t 分布中有一个重要的概念——自由度，其值为。为什么是呢？我拿样本方差的计算过程来说明吧，样本方差为

当个样本均值确定时，如果知道了其中的任意个样本的值，那么剩下的一个样本的值自然就确定了，这就是为什么自由度为。这里还是在贴一次t分布的概率表吧。

​

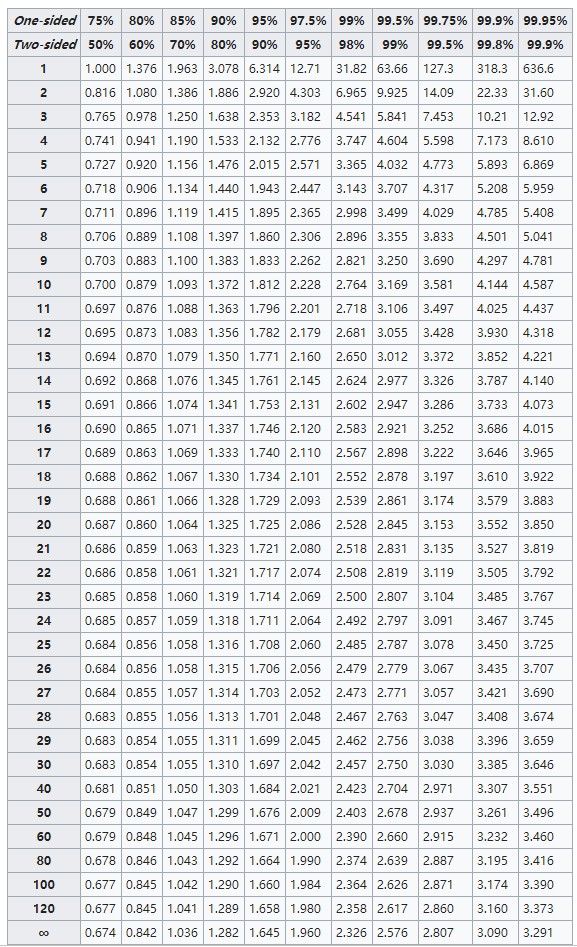
4. t 检验

       现在我们再回到一开始的“比较麦子种植工艺A和B的优劣比较”问题，   William Sealy Gosset提出的问题是：这20的差值是否在工艺A下麦子平均产量的正常波动范围内？这实际上是一个双样本的 t 检验问题，不过可以将其转化为单样本的 t 检验问题，认为工艺B下麦子的均值也为100，即然后看一下这20的差值是否是显著的。现在我们提出如下假设

:  工艺B与工艺A下大麦产量一致

上面的例子中没有给出工艺B下麦子产量的标准差，我这里先假设一个，为，那么可以按照单样本的 t 统计量定义式计算此时的统计量值

选定 95%的置信水平，自由度为99（样本个数为100），查 t 概率分布表得到1.660（自由度99与自由度100接近，我这里就按100算了），这远小于17.889，因此我们有理由拒绝接受原假设，从而认为工艺B提升了麦子的产量。

5. 小结

       对于 t 检验，我还想再说两句，不管是独立样本还是相依样本的 t 检验，目的都是为了判断两类样本在某一变量上的均值差异是否显著，这也是构造 t 检验的作用。