AtCoder Beginner Contest 183 E - Queen on Grid (DP)

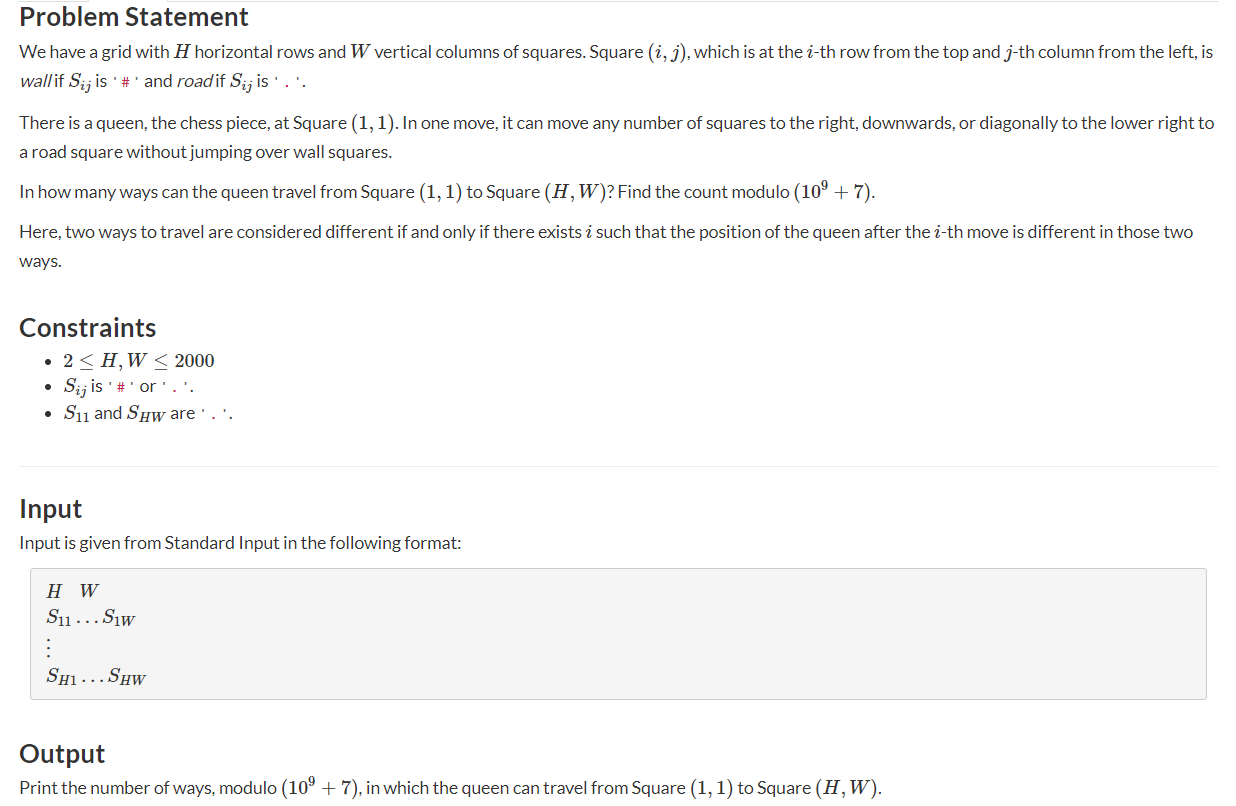
• 题意:有一个\(n\)x\(m\)的棋盘,你需要从\((1,1)\)走到\((n,m)\),每次可以向右,右下,下走任意个单位,\(.\)表示可以走,#表示一堵墙,不能通过,问从\((1,1)\)走\((n,m)\)的方案数.

• 题解:走棋盘的经典问题的改编,唯一不同的地方在于,棋子可以在某一方向移动任意距离,而某一点的状态可以从上,左上,左三个方向的任意一个\(.\)的点转移而来,所以我们可以记这三个方向的前缀和,然后写出状态转移方程,我们记\(dp[0][i][j]\)为横向的前缀和,同理,\(1\)表示斜向,\(2\)表示纵向,而\(3\)则表示当前点的方案数,假设左方向表示为\(0\),则:\(dp[0][i][j]=dp[0][i-1][j]+dp[3][i-1][j]\),其他两个方向也是同理,求出三个方向的前缀和后再更新当前点的状态,\(dp[3][i][j]=dp[0][i][j]+dp[1][i][j]+dp[2][i][j]\).

• 代码:

  #define int long long 
  
  int n,m;
  char g[2010][2010];
  int dp[4][2010][2010];
  
  signed main() {
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      cin>>n>>m;
  
      rep(i,1,n){
      	rep(j,1,m){
      		cin>>g[i][j];
      	}
      }
  
      dp[3][1][1]=1;
  
      rep(i,1,n){
      	rep(j,1,m){
      		if(g[i][j]=='.' && i+j!=2){
      			dp[0][i][j]=(dp[0][i-1][j]+dp[3][i-1][j])%mod;
      			dp[1][i][j]=(dp[1][i-1][j-1]+dp[3][i-1][j-1])%mod;
      			dp[2][i][j]=(dp[2][i][j-1]+dp[3][i][j-1])%mod;
      			dp[3][i][j]=(dp[0][i][j]+dp[1][i][j]+dp[2][i][j])%mod;
      		}
      	}
      }
  
      cout<<dp[3][n][m]<<'\n';
  
      return 0;
  }