【CF1445D】Divide and Sum 题解

题目链接

题意简介

将一个长度为 2n 的数列平均分为两个子数列 p 和 q 后，p 按从小到大排序，q 按从大到小排序。

排序后，记 p 为 \(\{x_i\}\) ，q 为 \(\{y_i\}\) ，对每种划分方式，有 \(f(p,q) = \sum |x_i - y_i|\)

现在我们想要知道对所有的划分方案 \((p,q)\) ，\(\sum f(p,q)\) 是多少。

数据范围：\(1 \leq n \leq 150000\) 答案对 998244353 取模。

Two partitions of an array are considered different if the sets of indices of elements included in the subsequence p are different.

这句话可以这么理解，就算元素的值相同，只要它们在原数列中的下标不同，就算为不同的元素。

只要原列组中有一个元素的所处位置( p 或 q )不同，就视为两种划分方式不同。

思路分析

考虑暴力，我们会发现我们共需要讨论 \({2n \choose n}\) 种情况，显然不能这么算。

(上面那个是组合数公式 2n 选 n)

于是我们自然而然地想到，既然对每种划分情况行不通，我们就考虑把每个数分开来，讨论其对于答案的贡献。

通过对式子的观察，我们可以得出结论：\(x_i,y_i\) 中较大值对答案贡献为正，较小值对答案贡献为负。

首先对原数列做排序处理。

现在我们对原数列进行从小到大排序，考虑从左到右选到第 i 个数 \(a_i\) 时，之前选了 \(k\) 个数在数列 q 中，\(i-1-k\) 个数在 p 中的情形。

(为避免重复计算与讨论的麻烦，不妨假设排序时，对于值相同的元素，在 \(\{a_i\}\) 中的下标越小越小。)

于是我们知道，前 i-1 个数都比 \(a_i\) 小。

由于我们从左到右选数，我们不难看出，每选到一个数加入数列 q，这个数将从右往左地添加到 q 中。而如果是加入数列 p，这个数将被从左往右地加入 p 中。如下图：

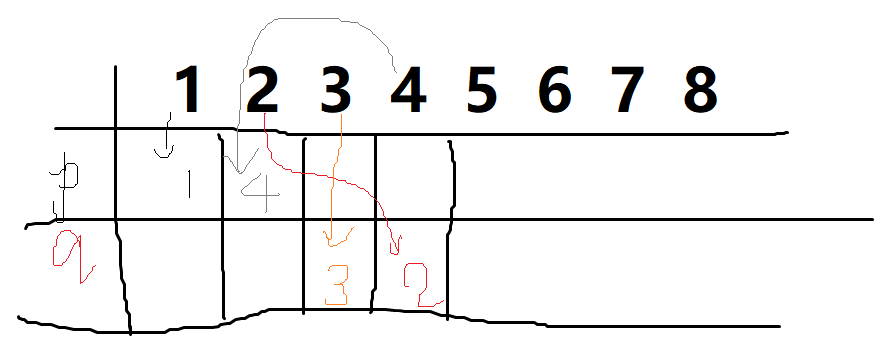
接下来我们分析，假定我们希望将 \(a_i\) 选入 p 中，那么 \(a_i\) 对应的实际上就是 \(x_{i-1-k}\)，想要这个数对答案的贡献为正，我们就需要使其对应的 \(y_{i-1-k}\) 比它小。由于我们已经将原数列排序，所以这个 \(y_{i-1-k}\) 在原数列中对应的 \(a_j\) 应有 \(j<i\) 。

而前面的数的选择我们实际上已经决定好了：我们选了 k 个数在 q 中。所以，我们必须要求这 k 个数中的某个数对于的 \(y_i\) 下标等于 \(i-1-k\) 。如下图。

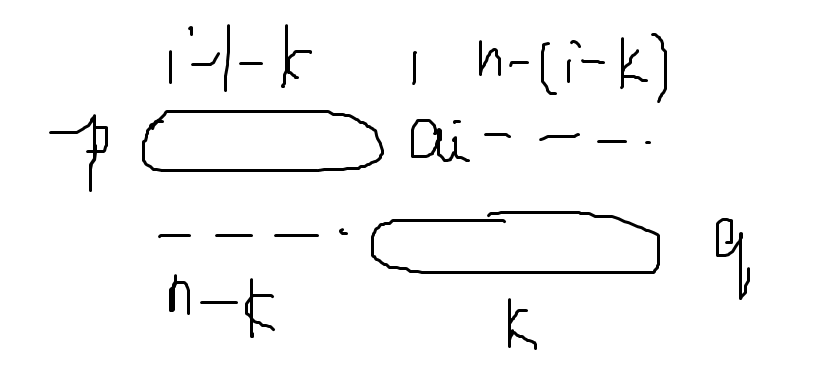
显然，只有当 \(k\geq n-(i-k)+1\) 时，\(a_i\) 对答案的贡献为正。

经过简单的化简，我们得出 \(i > n\) 这样一条与 k 无关的式子。

换句话说，只要满足 \(i > n\) ，任何的将 \(a_i\) 放在 \(p\) 的情形，\(a_i\) 对答案的贡献都是正的。反之，贡献为负。

同理，假如我们考虑把 \(a_i\) 放到 q 中，同理，假如我们希望其贡献为正，那么 \(a_i\) 对应的 \(y_j\) 所对应的 \(x_j\) 所对应的 \(a_l\) 的下标应该出现在 i 之前，也就是比 \(a_i\) 小。

上面这句话可能有点绕。如下图。

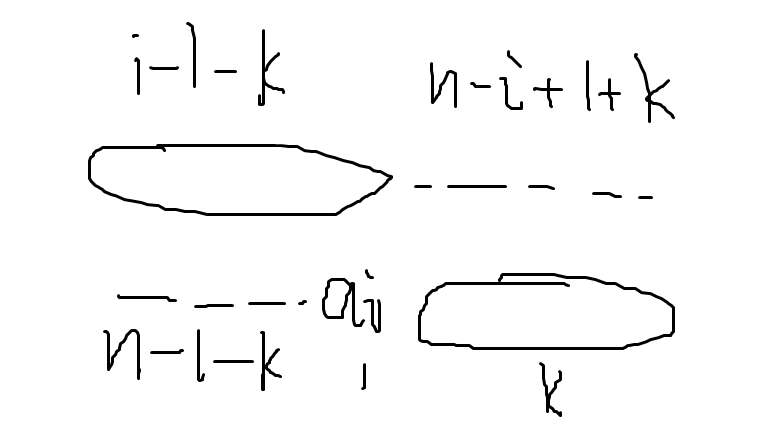
显然，只有当 \(i-1-k \geq n-1-k+1\) 时，\(a_i\) 对答案的贡献为正。

化简后，我们又得到了同一条式子：\(i > n\) 。

于是，我们得出结论，无论怎么分，只要 \(i>n\) ，\(a_i\) 对答案的贡献就是正的，反之则是负的。

所以，答案就是 \({2n \choose n} \times (\sum_{i=n+1}^{2n} a_i - \sum_{i=1}^{n} a_i)\)

代码库

#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
#define REG register
#define rep(i,a,b) for(REG int i=a;i<=b;i++)
const int N=3e5+5,mod=998244353;
int A[N],n; ll fac[N],ans1,ans2;
inline ll _pow(ll x,int p){
    REG ll ans=1;
    while(p) (p&1)&&(ans=ans*x%mod),x=x*x%mod,p>>=1;
    return ans;
}
inline ll _inv(ll x){
    return _pow(x,mod-2);
}
inline ll C(ll a,ll b){
    return fac[a]*_inv(fac[b])%mod*_inv(fac[a-b])%mod;
}
int main(){
    scanf("%d",&n);
    rep(i,1,n<<1) scanf("%d",A+i);
    sort(A+1,A+(n<<1)+1);
    fac[0]=1;
    rep(i,1,n<<1) fac[i]=fac[i-1]*i%mod;
    ll temp=C(n<<1,n);
    rep(i,1,n) ans1=(ans1+A[i]*temp)%mod;
    rep(i,n+1,n<<1) ans2=(ans2+A[i]*temp)%mod;
    printf("%lld\n",(-ans1+ans2+mod)%mod);
    return 0;
}