Java数据结构——图的基本理论及简单实现

1. 图的定义
图(graph)是由一些点(vertex)和这些点之间的连线(edge)所组成的；其中，点通常被成为"顶点(vertex)"，而点与点之间的连线则被成为"边或弧"(edege)。通常记为，G=(V,E)。

2. 图的种类
根据边是否有方向，将图可以划分为：无向图和有向图。

2.1 无向图

（以下图片来自网络）

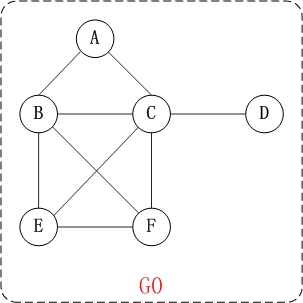
上面的图G0是无向图，无向图的所有的边都是不区分方向的。G0=(V1,{E1})。其中，
(01) V1={A,B,C,D,E,F}。 V1表示由"A,B,C,D,E,F"几个顶点组成的集合。
(02) E1={(A,B),(A,C),(B,C),(B,E),(B,F),(C,F), (C,D),(E,F),(C,E)}。 E1是由边(A,B),边(A,C)...等等组成的集合。其中，(A,C)表示由顶点A和顶点C连接成的边。

2.2 有向图

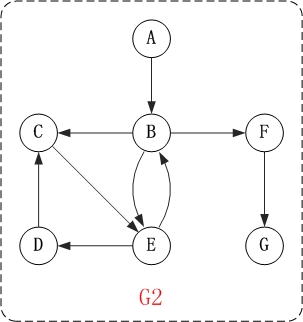
上面的图G2是有向图。和无向图不同，有向图的所有的边都是有方向的！ G2=(V2,{A2})。其中：
(01) V2={A,C,B,F,D,E,G}。 V2表示由"A,B,C,D,E,F,G"几个顶点组成的集合。
(02) A2={<A,B>,<B,C>,<B,F>,<B,E>,<C,E>,<E,D>,<D,C>,<E,B>,<F,G>}。 E1是由矢量<A,B>,矢量<B,C>...等等组成的集合。其中，矢量<A,B)表示由"顶点A"指向"顶点C"的有向边。

3. 邻接点和度

3.1 邻接点
一条边上的两个顶点叫做邻接点。

例如，上面无向图G0中的顶点A和顶点C就是邻接点。
在有向图中，除了邻接点之外；还有"入边"和"出边"的概念。
顶点的入边，是指以该顶点为终点的边。而顶点的出边，则是指以该顶点为起点的边。
例如，上面有向图G2中的B和E是邻接点；<B,E>是B的出边，还是E的入边。

3.2 度
在无向图中，某个顶点的度是邻接到该顶点的边(或弧)的数目。
例如，上面无向图G0中顶点A的度是2。
在有向图中，度还有"入度"和"出度"之分。
某个顶点的入度，是指以该顶点为终点的边的数目。而顶点的出度，则是指以该顶点为起点的边的数目。
顶点的度=入度+出度。
例如，上面有向图G2中，顶点B的入度是2，出度是3；顶点B的度=2+3=5。

4. 路径和回路

1. 路径：如果顶点(Vm)到顶点(Vn)之间存在一个顶点序列。则表示Vm到Vn是一条路径。
2. 路径长度：路径中"边的数量"。
3. 简单路径：若一条路径上顶点不重复出现，则是简单路径。
4. 回路：若路径的第一个顶点和最后一个顶点相同，则是回路。
5. 简单回路：第一个顶点和最后一个顶点相同，其它各顶点都不重复的回路则是简单回路。

5. 连通图和连通分量

1. 连通图：对无向图而言，任意两个顶点之间都存在一条无向路径，则称该无向图为连通图。 对有向图而言，若图中任意两个顶点之间都存在一条有向路径，则称该有向图为强连通图。
2. 连通分量：非连通图中的各个连通子图称为该图的连通分量。

6. 权
在学习"哈夫曼树"的时候，了解过"权"的概念。图中权的概念与此类似。

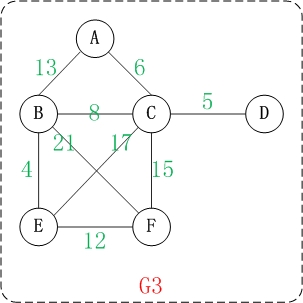
上面就是一个带权的图。

7. 图的存储结构

7.1. 邻接矩阵
邻接矩阵是指用矩阵来表示图。它是采用矩阵来描述图中顶点之间的关系(及弧或边的权)。
假设图中顶点数为n，则邻接矩阵定义为：

下面通过示意图来进行解释。

图中的G1是无向图和它对应的邻接矩阵。

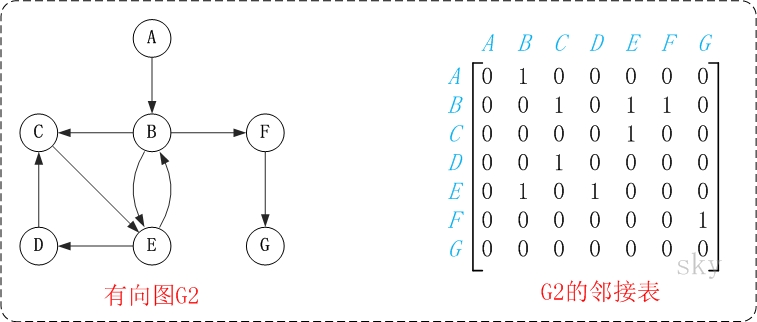
图中的G2是无向图和它对应的邻接矩阵。
通常采用两个数组来实现邻接矩阵：一个一维数组用来保存顶点信息，一个二维数组来用保存边的信息。
邻接矩阵的缺点就是比较耗费空间。

6.2. 邻接表
邻接表是图的一种链式存储表示方法。它是改进后的"邻接矩阵"，它的缺点是不方便判断两个顶点之间是否有边，但是相对邻接矩阵来说更省空间。

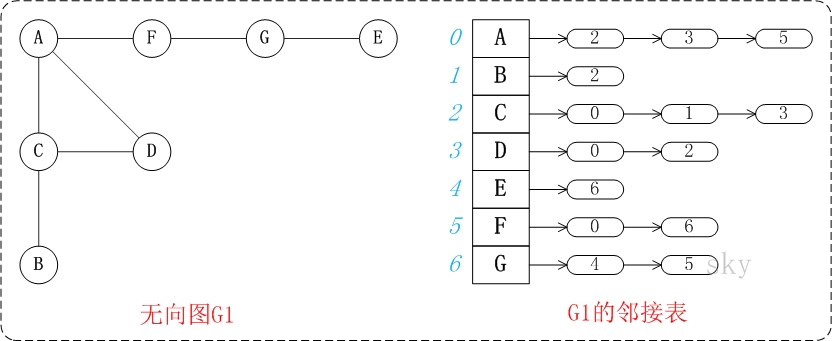
图中的G1是无向图和它对应的邻接矩阵。

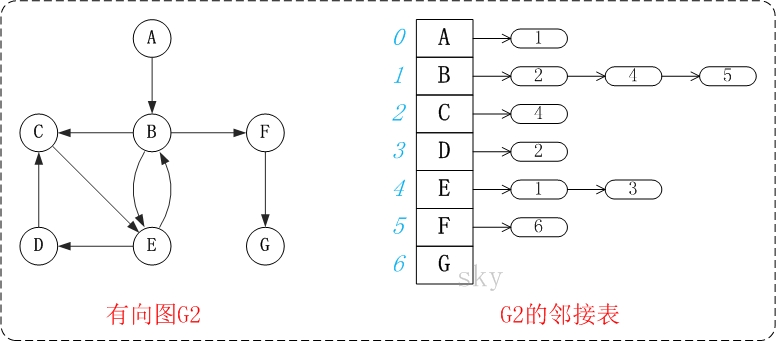
图中的G2是无向图和它对应的邻接矩阵。

8. Java代码实现求图的出度和入度

public class Graph {
private int size; // 顶点数量
private int[] vertexs; // 顶点数组
private int[][] matrix; // 邻接矩阵
private static final int MAX_WEIGHT = 10000;

public Graph(int size) {
super();
this.size = size;
vertexs = new int[size];
for (int i = 0; i < size; i++) {
vertexs[i] = i;
}
matrix = new int[size][size];
}

public int getSize() {
return size;
}

public void setSize(int size) {
this.size = size;
}

public int[] getVertexs() {
return vertexs;
}

public void setVertexs(int[] vertexs) {
this.vertexs = vertexs;
}

// 出度
public int outDegree(int index) {
int degree = 0;
for (int i = 0; i < matrix[index].length; i++) {
int weight = matrix[index][i];
if (weight != 0 && weight != MAX_WEIGHT) {
degree++;
}
}
return degree;
}

// 入度
public int inDegree(int index) {
int degree = 0;
for (int i = 0; i < matrix.length; i++) {
int weight = matrix[i][index];
if (weight != 0 && weight != MAX_WEIGHT) {
degree++;
}
}
return degree;
}

// 获取权值
public int getWeight(int v1, int v2) {
int weight = matrix[v1][v2];
return weight == 0 ? 0 : (weight == MAX_WEIGHT ? -1 : weight);
}

// 获取最大出度
public int maxOutDegree() {
int maxDegree = 0;
for (int i = 0; i < matrix.length; i++) {
int degree = outDegree(i);
if (maxDegree < degree) {
maxDegree = degree;
}
}
return maxDegree;
}

// 获取最大入度
public int maxInDegree() {
int maxDegree = 0;
for (int i = 0; i < matrix[0].length; i++) {
int degree = inDegree(i);
if (maxDegree < degree) {
maxDegree = degree;
}
}
return maxDegree;
}

public static void main(String[] args) {
Graph graph = new Graph(5);
int[] a0 = new int[] { 0, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 6 };
int[] a1 = new int[] { 9, 0, 3, MAX_WEIGHT, MAX_WEIGHT };
int[] a2 = new int[] { 2, MAX_WEIGHT, 0, 5, MAX_WEIGHT };
int[] a3 = new int[] { 0, MAX_WEIGHT, MAX_WEIGHT, 0, 1 };
int[] a4 = new int[] { 0, MAX_WEIGHT, MAX_WEIGHT, MAX_WEIGHT, 0 };
graph.matrix[0] = a0;
graph.matrix[1] = a1;
graph.matrix[2] = a2;
graph.matrix[3] = a3;
graph.matrix[4] = a4;

System.out.println("v0的出度：" + graph.outDegree(0));
System.out.println("v0的入度：" + graph.inDegree(0));
System.out.println("v0到v1的权值：" + graph.getWeight(0, 1));
System.out.println("v1到v0的权值：" + graph.getWeight(1, 0));
System.out.println("最大出度：" + graph.maxOutDegree());
System.out.println("最大入度：" + graph.maxInDegree());
}
}