[Fundamental of Power Electronics]-PART II-7. 交流等效电路建模-7.3 脉冲宽度调制器建模

7.3 脉冲宽度调制器建模

我们现在已经达成了本章开始的目标，为图7.1推导了一个有效的等效电路模型。但仍存在一个细节，对脉冲宽度调制(PWM)环节进行建模。如图7.1所示的脉冲宽度调制器可以产生一个能够控制功率晶体管开关或导通的逻辑信号\(\delta(t)\)。该逻辑信号\(\delta(t)\)是周期性的，且其频率为\(f_{s}\)，占空比为\(d(t)\)。脉冲宽度调制器的输入是一个模拟控制信号\(v_{c}(t)\)。脉冲宽度调制器的功能为产生一个正比于模拟控制电压\(v_{c}(t)\)的占空比\(d(t)\)。这里的\(\delta (t)\)就是\(c(t)\)。

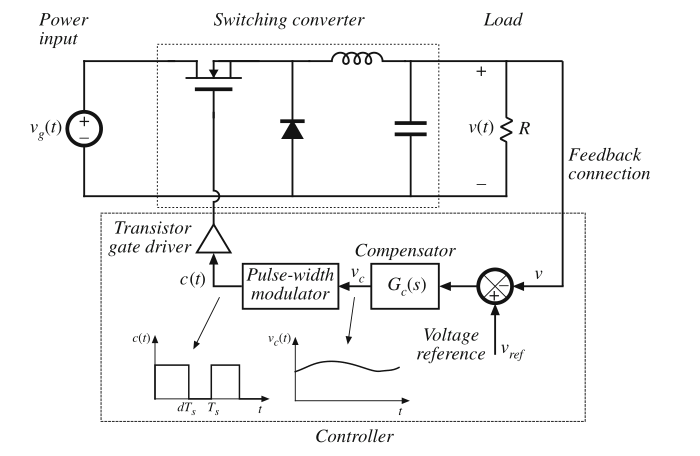
Fig 7.1

图7.29给出了一个简单的脉冲宽度调制器的原理图，其中锯齿波发生器产生如图7.30所示的电压波形\(V_{saw}(t)\)。该波形的峰峰值为\(V_{M}\)。变换器的开关频率\(f_{s}\)取决并等于锯齿波\(V_{saw}(t)\)的频率。模拟比较器对控制电压信号\(v_{c}(t)\)和\(V_{saw}(t)\)进行比较。该比较器产生逻辑电平输出，其中当\(v_{c}(t)\)大于\(v_{saw}(t)\)时输出高电平，反之则输出低电平。典型的波形如图7.30所示。

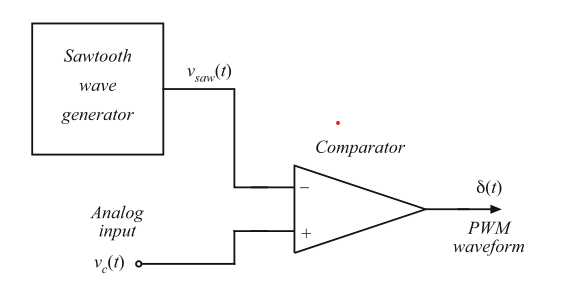
Fig. 7.29 A simple pulse-width modulator circuit

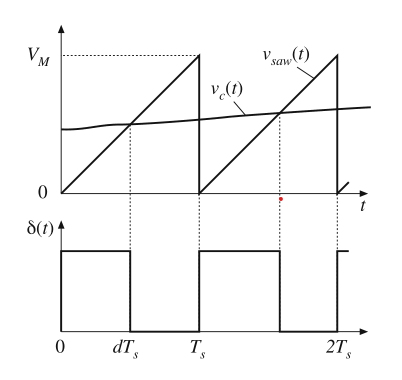
Fig. 7.30 Waveforms of the circuit of Fig.7.29

如果锯齿波\(v_{saw}(t)\)的最小值为0，那么当\(v_{c}(t)\)小于或者等于0时，占空比都将是0。而当\(v_{c}(t)\)大于\(V_{M}\)时，占空比\(D=1\)。如果在给定的开关周期内，\(v_{saw}(t)\)随着时间\(t\)线性变化，那么当\(0 \leq v_{c}(t) \leq V_{M}\)时，占空比\(d\)将会是\(v_{c}\)的线性函数。因此可以写出：

\[d(t)= \frac{v_{c}(t)}{V_{M}}\ \ \ for\ 0 \leq v_{c}(t) \leq V_{M} \tag{7.82}
\]

这个公式就是脉冲宽度调制器的输入输出特性。

为了与前面各节中变换器的扰动与线性化模型保持一致，我们对式(7.82)进行扰动：

\[v_{c}(t)=V_{c}+\hat{v}_{c}(t) \\
d(t)=D+\hat{d}(t) \tag{7.83}
\]

将式(7.83)代入式(7.82)得到：

\[D+\hat{d}(t)=\frac{V_{c}+\hat{v}_{c}(t)}{V_{M}} \tag{7.84}
\]

表示式(7.84)的框图如图7.31所示。脉冲宽度调制器具有线性增益\(1/V_{M}\)。通过对式(7.84)左右同类项相等，可以得到：

\[D=\frac{V_{c}}{V_{M}} \\
\hat{d}(t)=\frac{\hat{v}_{c}(t)}{V_{M}} \tag{7.85}
\]

因此，占空比的静态值是由\(V_{c}\)确定的。

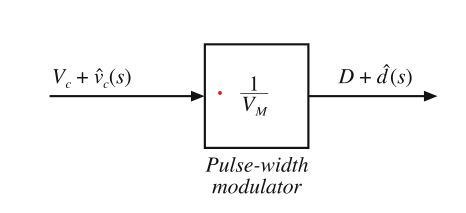
Fig. 7.31 Pulse-width modulator block diagram

图7.31所示的脉冲宽度调制器模型几乎对所有应用都足够准确。必须指出的是，脉冲宽度调制器同时也引入了对波形的采样过程。尽管模拟输入信号\(v_{c}(t)\)是时间的连续函数，但在每个开关周期内，占空比只能是一个离散的值。因此，脉冲宽度调制器以等于开关频率\(f_{s}\)的采样率对波形进行采样。所以，一个更加精确的调制器模型如图7.32所示。在小信号意义上，脉冲宽度调制器中的采样发生在PWM信号的调制沿上。例如，在以图7.30所示的波形为例的后沿PWM中，采样时刻PWM输出信号\(\delta (t)\)的下降沿一致。这对于采样-数据(Sampled-Data)动态模型的建立具有重要意义，在这种模型中，变换器对占空比扰动的响应被建模为等效保持(equivalent hold)。在15.5节中DCM变换器的高频模型和18.7的电流程控模型建立中考虑了脉冲宽度调制器的Sample-data特性。如第19章所述，PWM采样性质在应用数字控制的变换器的环路控制的延时中具有重要影响。

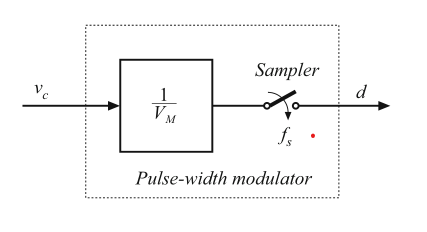
Fig. 7.32 A more accurate pulse-width modulator model, including sampling

实际上，PWM采样将交流小信号的可用频率限制在了远小于开关频率的值。设计者必须保证控制系统的带宽远小于奈奎斯特频率\(f_{s}/2\)。控制信号\(v_{c}(t)\)中的明显的高频变化也会改变脉冲宽度调制器的表现。一个典型的例子就是由于反馈回路引入，使得控制信号\(v_{c}(t)\)含有开关纹波。很多研究人员已经分析过这种问题(A.R. Brown, R.D. Middlebrook, Sampled-data modeling of switching regulators, in IEEE Power Electronics Specialists Conference (PESC 1981), pp. 349–369, June 1981),(D.J. Shortt, F.C. Lee, Extensions of the discrete-average models for converter power stages, in IEEE Power Electronics Specialists Conference (PESC 1983), pp. 23–37, June 1983)，并且，电感电流纹波对电流编程控制变换器的传递函数的影响也在第18章中进行了研究。但是通常最好避免\(v_{c}(t)\)包含较多的开关频率或更高频率下的纹波，因为这类系统的脉冲宽度调制器的高频抗扰特性较差。