883. Projection Area of 3D Shapes

问题

NxN个格子中，用1x1x1的立方体堆叠，grid[i][j]表示坐标格上堆叠的立方体个数，求三视图面积。

Input: [[1,2],[3,4]]

Output: 17

Explanation: 见下图

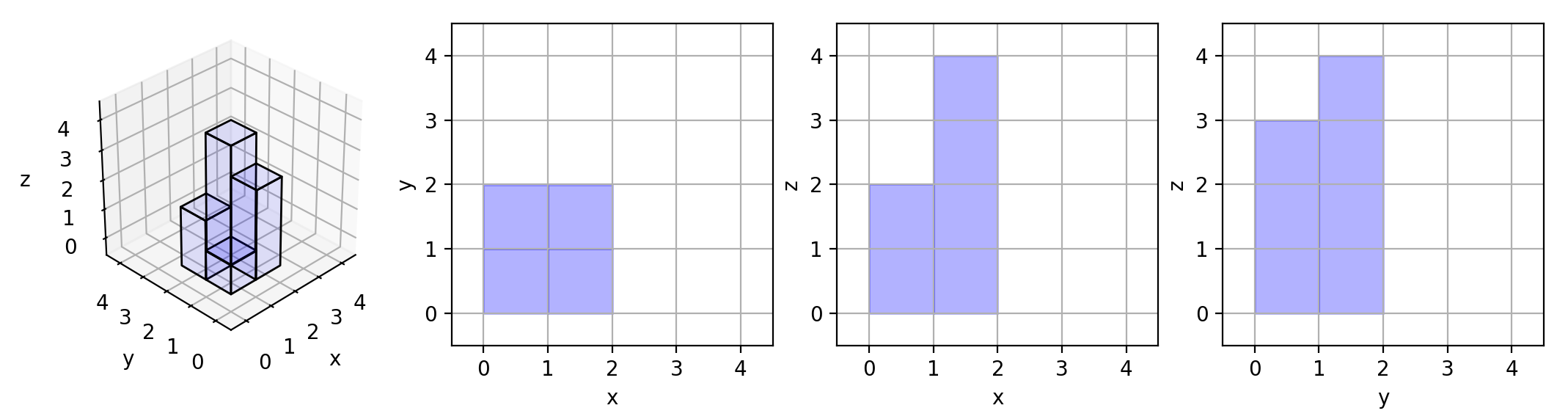
思路

对于俯视图，只要一个格子有值，面积值就加1。

对于正视图（面朝x轴），对于某一个x，在y轴方向上拥有的最高grid值，表示，该x顺着y轴看过去看到的面积值。

对于侧视图（面朝y轴），对于某一个y，在x轴方向上拥有的最高grid值，表示，该y顺着y轴看过去看到的面积值。

把这些面积值加起来即可。

时间复杂度O(n^2，空间复杂度O(1)

代码

class Solution(object):
    def projectionArea(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        s = 0
        n = len(grid)
        for i in range(n):
            best_row = 0
            best_col = 0
            for j in range(n):
                if(grid[i][j] > 0):
                    s += 1
                best_row = max(best_row, grid[i][j])
                best_col = max(best_col, grid[j][i])
            s += best_row + best_col
        return s

类似题目

892. Surface Area of 3D Shapes