Dijkstra算法（C语言）

Dijkstra算法

1.定义概览

Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法，用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法，在很多专业课程中都作为基本内容有详细的介绍，如数据结构，图论，运筹学等等。注意该算法要求图中不存在负权边。

2.算法描述

1)算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

2)算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

3.算法代码实现：

const int  MAXINT = ;
const int MAXNUM =  ;
int dist[MAXNUM];
int prev[MAXNUM];

int A[MAXUNM][MAXNUM];

void Dijkstra(int v0)
{
  　　bool S[MAXNUM];                                  // 判断是否已存入该点到S集合中
      int n=MAXNUM;
  　　for(int i=; i<=n; ++i)
 　　 {
      　　dist[i] = A[v0][i];
      　　S[i] = false;                                // 初始都未用过该点
      　　if(dist[i] == MAXINT)
            　　prev[i] = -;
 　　     else
            　　prev[i] = v0;
   　　}
   　 dist[v0] = ;
   　 S[v0] = true; 　　
 　　 for(int i=; i<=n; i++)
 　　 {
       　　int mindist = MAXINT;
       　　int u = v0; 　　                            // 找出当前未使用的点j的dist[j]最小值
      　　 for(int j=; j<=n; ++j)
      　　    if((!S[j]) && dist[j]<mindist)
      　　    {
         　　       u = j;                             // u保存当前邻接点中距离最小的点的号码
         　 　      mindist = dist[j];
       　　   }
       　　S[u] = true;
       　　for(int j=; j<=n; j++)
       　　    if((!S[j]) && A[u][j]<MAXINT)
       　　    {
           　    　if(dist[u] + A[u][j] < dist[j])     //在通过新加入的u点路径找到离v0点更短的路径
           　    　{
                   　　dist[j] = dist[u] + A[u][j];    //更新dist
                   　　prev[j] = u;                    //记录前驱顶点
            　　    }
        　    　}
   　　}
}

4.算法实例

先给出一个无向图

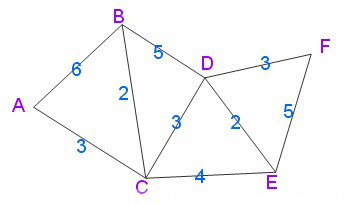
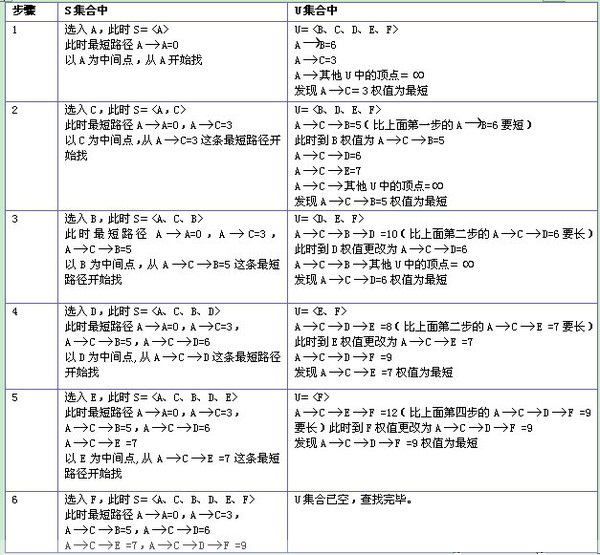
用Dijkstra算法找出以A为起点的单源最短路径步骤如下