hdu6415 Rikka with Nash Equilibrium (DP)

题目链接

Problem Description

Nash Equilibrium is an important concept in game theory. Rikka and Yuta are playing a simple matrix game. At the beginning of the game, Rikka shows an $$$n\times m$$$ integer matrix A. And then Yuta needs to choose an integer in $$$[1,n]$$$, Rikka needs to choose an integer in $$$[1,m]$$$. Let $$$i$$$ be Yuta's number and $$$j$$$ be Rikka's number, the final score of the game is $$$A_{i,j}$$$. In the remaining part of this statement, we use $$$(i,j)$$$ to denote the strategy of Yuta and Rikka. For example, when $$$n=m=3$$$ and matrix $$$A$$$ is $$$$$$ \begin{bmatrix} 1 & 1 & 1 \\ 2 & 4 & 1 \\ 1 & 3 & 1 \\ \end{bmatrix} $$$$$$ If the strategy is $$$(1,2)$$$, the score will be $$$2$$$; if the strategy is $$$(2,2)$$$, the score will be $$$4$$$. A pure strategy Nash equilibrium of this game is a strategy $$$(x,y)$$$ which satisfies neither Rikka nor Yuta can make the score higher by changing his(her) strategy unilaterally. Formally, $$$(x,y)$$$ is a Nash equilibrium if and only if: $$$$$$\begin{cases} A_{x,y}≥A_{i,y}, & {\forall i \in [1,n]} \\[1ex] A_{x,y}≥A_{x,j}, & {\forall j \in [1,m]} \end{cases}$$$$$$ In the previous example, there are two pure strategy Nash equilibriums: $$$(3,1)$$$ and $$$(2,2)$$$. To make the game more interesting, Rikka wants to construct a matrix $$$A$$$ for this game which satisfies the following conditions: 1. Each integer in $$$[1,nm]$$$ occurs exactly once in $$$A$$$. 2. The game has at most one pure strategy Nash equilibriums. Now, Rikka wants you to count the number of matrixes with size $$$n×m$$$ which satisfy the conditions.

Input

The first line contains a single integer $$$t(1≤t≤20)$$$, the number of the testcases.

The first line of each testcase contains three numbers $$$n$$$,$$$m$$$ and $$$K$$$ $$$(1≤n,m≤80,1≤K≤10^9)$$$.

The input guarantees that there are at most $$$3$$$ testcases with max$$$(n,m)>50$$$.

Output

For each testcase, output a single line with a single number: the answer modulo K.

Sample Input

2
3 3 100
5 5 2333

Sample Output

64
1170

题意

求符合条件的n*m的矩阵的个数，要求1~n*m每个数只用一次，且只能有一个位置满足同时是所在行和列最大的数

分析

最大的数是n*m，它比所有数都大，所以n*m永远是它所在行和列最大的数，同时也因为它一定是最大的，所以它的安放不受任何限制。
假设已经给n*m安排了一个位置，那么n*m-1就是剩下的数中最大的，但是他的安放收到限制，不能再让他同时满足行列最大。观察发现，它只有在n*m同行或同列时，它才不是这行或这一列最大的，也就是说n*m-1必须和n*m同行或同列。接下来n*m-2也是同理，必须和n*m或n*m-1其中一个同行或同列。
因此，为了构造合法的矩阵，优先考虑的是当前最大的数，所以应该按照从大到小的顺序来填充。只要保证每个数都与之前的数中的某一个同行同列，那么构造出来的所有矩阵都是合法的。
如果换个角度来看问题就是这样，每次操作都有若干个位置可以选择，而每次给一个数安排一个位置，就相当于把所在的行和列，加入到下一个数的可选位置中。
容易发现，如果选择的位置所在行已经被添加过，那么可选位置只会增加列；如果所在列已经被添加过，那么只增加行；如果都被添加过了，那么这次安排就不会产生新的位置。根据增加的情况不同，可以把矩形划分成若干个区域，在某个区域中的任意位置安放数，增加的个数都是相同的。
为了方便分析，因为在同一区域中安放对最后求方案个数没有影响，可以规定每次只能选择区域左上角的位置。

比如说，第一个数有n*m种选择，但只考虑把它放到(1,1)，然后把第一行和第一列加入到可选择的位置；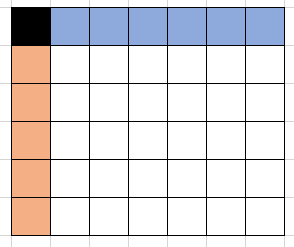

第二个数有n+m-1种选择，它可以放到与(1,1)相邻的(1,2)，或(2,1)
  或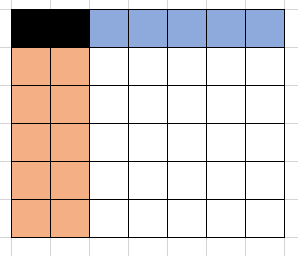 
后面的数以此类推

比较一般的情况：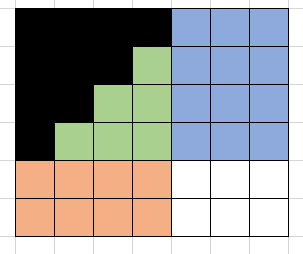

接下来的问题就是，需要维护的只有三个区域，观察发现，可以用三个指标来表示当前的状态：绿色区域的右下角的坐标（同时也是蓝色区域的左下角，橙色区域的右上角），以及已经在绿色区域填入了多少个数（用绿色区域的大小也能表示当前状态，但前者在状态转移的时候更为直观）。

对于(i, j, z)来说，下一个位置可以填在蓝色区域，橙色区域，绿色区域，对应能转移到的状态就是(i+1, j, z)，(i, j+1, z)，和(i, j, z+1)，其中，蓝色区域的大小为i*(m-j)，橙色区域的大小为j*(n-i)，绿色区域的大小为(i-1)*(j-1)-z，因此，如果用dp[i][j][z]记录(i, j, z)能产生的方案个数，那么就有dp[i][j][z]= i*(m-j)*dp[i+1][j][z] + j*(n-i)*dp[i][j+1][z]+ ((i-1)*(j-1)-z)*dp[i][j][z+1];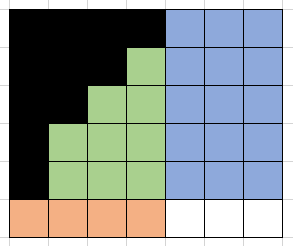
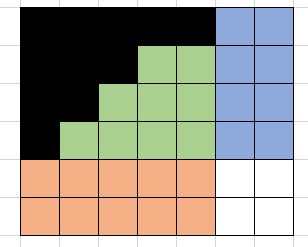
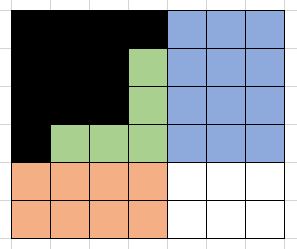       可以转移到的状态

注意到，一旦第一行或第一列完成填充，那么将不会再产生新的位置，或者换一句话说，所有位置都将变成可选位置，所以对于dp[n][j][z]或dp[i][m][z]而言，要考虑它能产生的方案数，其实就是它还剩下的位置数的阶乘。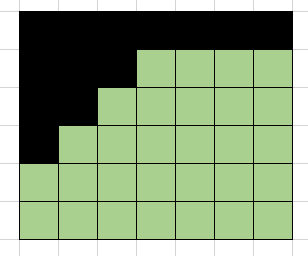
   剩下的位置可以以任意顺序填充

所以有：
dp[n][j][z]=(n*m-n-j+1-z)!
dp[i][m][z]=(n*m-i-m+1-z)!

从dp[n-1][m-1]开始，反向递推就能求出dp[1][1][0]

总结

本来最开始的时候，觉得数据量不大可以用dfs搜索一下的，后来发现搜索的时候有很多相同的状态，只要i, j, z都一样，那方案数就是一样的，于是加入记忆化搜索。后来写着，怎么觉得越看越像以前看过的推dp的样子，于是终于想到要用dp来做了。公式本身不算复杂，但是问题比较抽象，需要转化一下才好理解。

代码

#include<stdio.h>
#include<memory.h>

typedef long long LL;
int n, m;
LL mod;
int fac[];//阶乘打表
int dp[][][ * ];//已经处理到n行 m列 重叠部分填了z个
LL help;
void init() {
    memset(dp, , sizeof dp);
    fac[] = ;
    fac[] = ;
    //因为取模每次都在变，所以每次都要打表
    for (int t = ; t <= ; t++) {
        help = LL(t)*fac[t - ] % mod;
        fac[t] = help % mod;
    }
    //第一列全满的情况
    for (int j = ; j <= m; ++j) {
        for (int z = ; z <= (n-)*(j-); ++z)
            dp[n][j][z] = fac[n*m-n-j+ - z];
    }
    //第一行全满的情况
    for (int i = ; i <= n; ++i) {
        for (int z = ; z <=(m-)* ( i - ); ++z)
            dp[i][m][z] = fac[n*m-i-m+ - z];
    }
    //从dp[n-1][m-1]逆序递推
    for (int i = n - ; i >= ; --i) {
        for (int j = m - ; j >= ; --j) {
            for (int z = (i - )*(j - ); z >= ; --z) {

                help =   LL(n-i)*(j)*dp[i + ][j][z] /*下*/+
                         LL(m-j)*(i)*dp[i][j + ][z] /*右*/+
                         LL((i-)*(j-)-z)*dp[i][j][z + ] /*内*/;
                dp[i][j][z] = help % mod;
            }
        }
    }
}

int main() {
    int kase;
    for (scanf("%d", &kase); kase; kase--) {
        scanf("%d %d %lld", &n, &m, &mod);
        init();
        help = LL(n)*m*dp[][][];
        int ans = help%mod;
        printf("%d\n", ans);
    }

}