机器学习课程-第8周-降维(Dimensionality Reduction)—主成分分析(PCA)

1. 动机一：数据压缩

第二种类型的 无监督学习问题，称为 降维。有几个不同的的原因使你可能想要做降维。一是数据压缩，数据压缩不仅允许我们压缩数据，因而使用较少的计算机内存或磁盘空间，但它也让我们加快我们的学习算法。

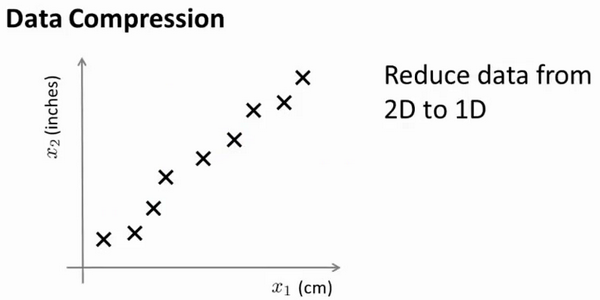
但首先，让我们谈论 降维是什么。作为一种生动的例子，我们收集的数据集，有许多，许多特征，我绘制两个在这里。

将数据从二维降一维：

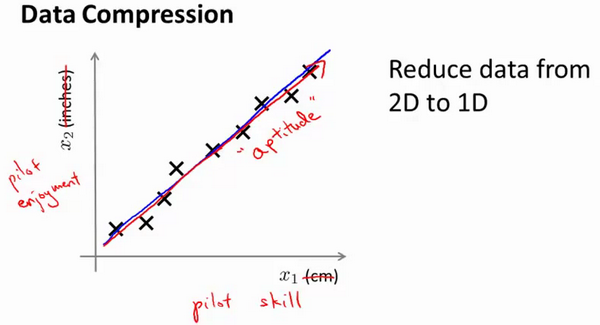
将数据从三维降至二维： 这个例子中我们要将一个三维的特征向量降至一个二维的特征向量。过程是与上面类似的，我们将三维向量投射到一个二维的平面上，强迫使得所有的数据都在同一个平面上，降至二维的特征向量。

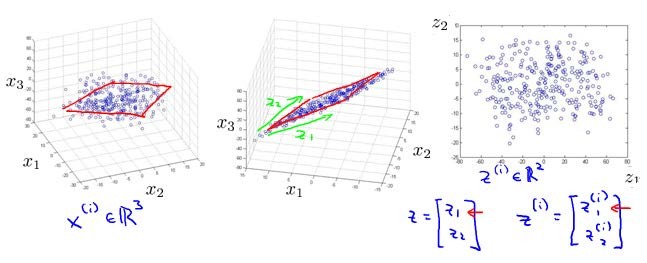
这样的处理过程可以被用于把任何维度的数据降到任何想要的维度，例如将1000维的特征降至100维。

2. 动机二：数据可视化

在许多及其学习问题中，如果我们能将数据可视化，我们便能寻找到一个更好的解决方案，降维可以帮助我们。

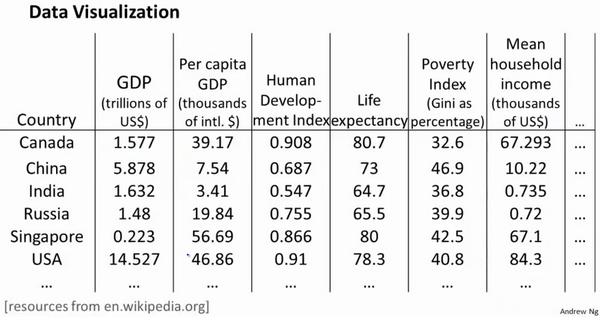
假使我们有有关于许多不同国家的数据，每一个特征向量都有50个特征（如GDP，人均GDP，平均寿命等）。

如果要将这个50维的数据可视化是不可能的。使用降维的方法将其降至2维，我们便可以将其可视化了。

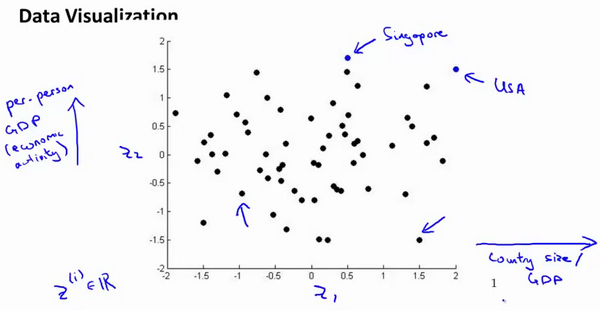
这样做的问题在于，降维的算法只负责减少维数，新产生的特征的意义就必须由我们自己去发现了。

3. 主成分分析问题

• 主成分分析(PCA)是最常见的降维算法。

• 在PCA中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据都投射到该向量上时，我们希望 投射平均均方误差 能尽可能地小。

• 方向向量：是一个经过原点的向量，而 投射误差 是 从特征向量 向该方向向量作垂线的长度。

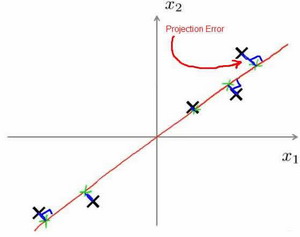
下面给出主成分分析问题的描述：

• 问题：将n维数据降至k维，目标是找到向量 $u^{(1)},u^{(2)},...,u^{(k)}$ 使得 总的投射误差最小。主成分分析与线性回顾的比较：

• 主成分分析与线性回归是两种不同的算法。主成分分析最小化的是 投射误差（Projected Error），而线性回归尝试的是最小化：预测误差。线性回归的目的是 预测结果，而主成分分析 不作任何预测。

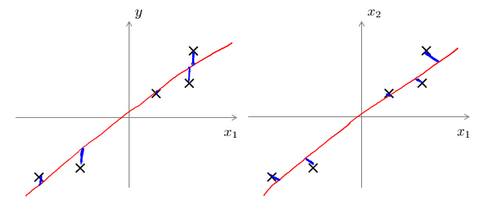
上图中，左边的是线性回归的误差（垂直于横轴投影），右边则是主要成分分析的误差（垂直于红线投影）。

• PCA：将n个特征降维到k个，可以用来进行数据压缩，如果100维的向量最后可以用10维来表示，那么压缩率为90%。同样图像处理领域的KL变换使用PCA做图像压缩。但PCA 要保证降维后，还要保证数据的特性损失最小。

• PCA技术好处：是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。

• PCA技术优点：它是完全无参数限制的。在PCA的计算过程中完全不需要人为的设定参数 或是 根据任何经验模型对计算进行干预，最后的 结果只与数据相关，与用户是独立的。

• 但是，这一点同时也可以看作是缺点。如果用户对观测对象有一定的先验知识，掌握了数据的一些特征，却无法通过参数化等方法对处理过程进行干预，可能会得不到预期的效果，效率也不高。

4. 主成分分析算法

PCA 减少n维到k维：

• 第一步：均值归一化。

  • 我们需要计算出所有特征的均值，然后令 $x_j= x_j-μ_j$。如果特征是在不同的数量级上，我们还需要将其除以 标准差 $σ^2$。

• 第二步：计算 协方差矩阵（covariance matrix）Σ：

  • $\sum=\dfrac {1}{m}\sum^{n}_{i=1}\left( x^{(i)}\right) \left( x^{(i)}\right) ^{T}$

• 第三步：计算 协方差矩阵Σ 的 特征向量（eigenvectors）:

  • 在 Matlab 里我们可以利用 奇异值分解（singular value decomposition）来求解，[U, S, V]= svd(sigma) 。

 $Sigma=\dfrac {1}{m}\sum^{n}_{i=1}\left( x^{(i)}\right) \left( x^{(i)}\right) ^{T}$

对于一个 $n×n$ 维度的矩阵，上式中的$U$：是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从 $n$ 维降至 $k$ 维，我们只需要从 $U$ 中选取前 $k$ 个向量，获得一个$n×k$ 维度的矩阵，我们用 $U_{reduce}$ 表示，然后通过如下计算获得要求的新特征向量 $z^{(i)}$:

$z^{(i)}=U^{T}_{reduce}*x^{(i)}$

 

其中 $x$ 是 $n×1$ 维的，因此结果为$k×1$维度。注，我们不对方差特征进行处理。