fjwc2019 D2T1 直径 （构造）

#181. 「2019冬令营提高组」直径

（这题构造题是我考场上唯一一A的题........）

先看这个特殊的Subtask4

Subtask 4（20pts）：$\sqrt{1+8k}$​​​ 为整数。

画了几张图，你轻松地发现这是菊花图。

大概就是这样↓

我们暂且设红点的个数为$k$表示菊花树的大小。

显然一棵菊花树的直径数为$k*(k-1)/2$

接下来我们试着以若干棵菊花图的形式构图。

当我们把两棵大小为（a,b）的菊花树连在一起时，

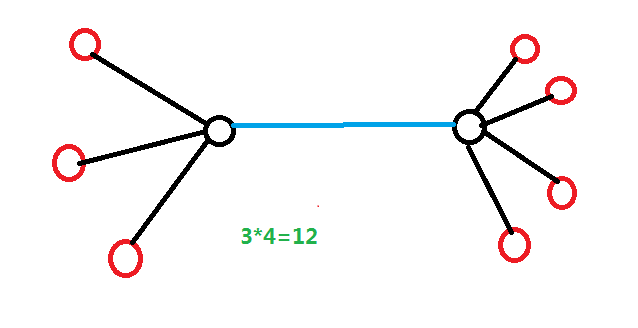
40pts到手

但是对于某些数（如一些大质数），两棵显然是不够的鸭

那么开三棵叭

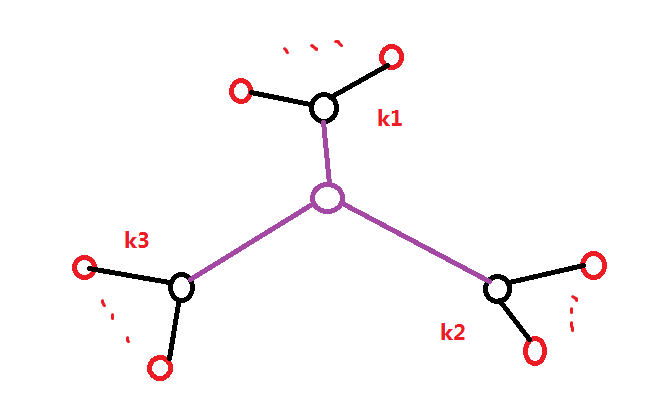
ans=k1*(k2+k3)+k2*k3，于是我们可以枚举其中两棵子树，推出剩下一棵是否符合条件。

打个code发现3棵树满足的范围远远超过5000000，瞎搞搞就解决了

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int k,ans,tp,A,B,C,cnt; bool ok;
int main(){
    freopen("diameter.in","r",stdin);
    freopen("diameter.out","w",stdout);
    scanf("%d",&k);
    if(k==){printf("2\n1 2 1\n");return ;}
    int sq=sqrt(*k+);
    if(sq*sq==*k+){
        for(int i=sqrt(*k);i*(i-)<=*k;++i)
            if(i*(i-)==*k){ans=i+;break;}
        printf("%d\n",ans);
        for(int i=;i<=ans;++i) printf("1 %d 1\n",i);
        return ;
    }//subtask 4
    if(k<=){
        ans=k+;
        printf("%d\n",ans);
        printf("1 2 233\n");
        for(int i=;i<=ans;++i) printf("1 %d 1\n",i);
        return ;
    }//subtask 1,2
    for(A=;A<=;++A){
        for(B=A;B<=;++B){
            int qwq=k-A*B;
            if(qwq<) continue;
            if(qwq%(A+B)!=) continue;
            C=qwq/(A+B);
            if(C<) continue;
            if(A+B+C+<=){ok=;break;}
        }
        if(ok)break;
    }
    ans=A+B+C+; cnt=;
    printf("%d\n",ans);
    for(int i=;i<=;++i) ++cnt,printf("1 %d 233\n",cnt);
    for(int i=;i<=A;++i) ++cnt,printf("2 %d 1\n",cnt);
    for(int i=;i<=B;++i) ++cnt,printf("3 %d 1\n",cnt);
    for(int i=;i<=C;++i) ++cnt,printf("4 %d 1\n",cnt);
    return ;
}