图的基本操作（基于邻接矩阵）：图的构造，深搜（DFS），广搜（BFS）

#include <iostream>
#include <stdio.h>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
using namespace std;  

typedef struct MGraph{
    string vexs[10];//顶点向量
    int arcs[10][10];//邻接矩阵
    int vexnum, arcnum;//图的顶点数和边数
}MGraph;  

int LocateVex(MGraph G, string u)//返回顶点u在图中位置
{
    for(int i=0; i<G.vexnum; i++)
        if(u==G.vexs[i])
            return i;
    return -1;
}  

void CreateUDG(MGraph &G)//构造无向图
{
    string v1,v2;
    int i, j, k;
    cout<<"请输入顶点数和边数：";
    cin>>G.vexnum>>G.arcnum;  

    cout<<"请输入顶点:";
    for(i=0; i<G.vexnum; i++)
        cin>>G.vexs[i];  

    for(i=0; i<G.vexnum; i++)
        for(j=0; j<G.vexnum; j++)
            G.arcs[i][j]=0;  

    cout<<"请输入边："<<endl;
    for(k=0; k<G.arcnum; k++)
    {
        cin>>v1>>v2;
        i=LocateVex(G, v1);
        j=LocateVex(G, v2);
        G.arcs[i][j]=G.arcs[j][i]=1;
    }
}  

void CreateUDN(MGraph &G)//构造无向网
{
    string v1, v2;
    int i, j, k;
    int w;
    cout<<"请输入顶点数和边数：";
    cin>>G.vexnum>>G.arcnum;  

    cout<<"请输入顶点:";
    for(i=0; i<G.vexnum; i++)
        cin>>G.vexs[i];  

    for(i=0; i<G.vexnum; i++)
        for(j=0; j<G.vexnum; j++)
            G.arcs[i][j]=-1000;  

    cout<<"请输入边："<<endl;
    for(k=0; k<G.arcnum; k++)
    {
        cin>>v1>>v2>>w;
        i=LocateVex(G, v1);
        j=LocateVex(G, v2);
        G.arcs[i][j]=G.arcs[j][i]=w;
    }
}  

void CreateDG(MGraph &G)//构造有向图
{
    string v1, v2;
    int i, j, k;
    cout<<"请输入顶点数和边数：";
    cin>>G.vexnum>>G.arcnum;  

    cout<<"请输入顶点:";
    for(i=0; i<G.vexnum; i++)
        cin>>G.vexs[i];  

    for(i=0; i<G.vexnum; i++)
        for(j=0; j<G.vexnum; j++)
            G.arcs[i][j]=0;  

    cout<<"请输入边："<<endl;
    for(k=0; k<G.arcnum; k++)
    {
        cin>>v1>>v2;
        i=LocateVex(G, v1);
        j=LocateVex(G, v2);
        G.arcs[i][j]=1;
    }
}  

void CreateDN(MGraph &G)//构造有向网
{
    string v1, v2;
    int i, j, k;
    int w;
    cout<<"请输入顶点数和边数：";
    cin>>G.vexnum>>G.arcnum;  

    cout<<"请输入顶点:";
    for(i=0; i<G.vexnum; i++)
        cin>>G.vexs[i];  

    for(i=0; i<G.vexnum; i++)
        for(j=0; j<G.vexnum; j++)
            G.arcs[i][j]=-1000;  

    cout<<"请输入边："<<endl;
    for(k=0; k<G.arcnum; k++)
    {
        cin>>v1>>v2>>w;
        i=LocateVex(G, v1);
        j=LocateVex(G, v2);
        G.arcs[i][j]=w;
    }
}  

int FirstAdjVex(MGraph G, int v)//返回顶点v的第一个邻接顶点序号
{
    for(int i=0; i<G.vexnum; i++)
        if(G.arcs[v][i]==1)
            return i;
    return -1;
}  

int NextAdjVex(MGraph G, int v, int w)//返回顶点v的相对于w的下一个邻接顶点序号
{
    for(int i=w+1; i<G.vexnum; i++)
        if(G.arcs[v][i]==1)
            return i;
    return -1;
}  

bool visited[100];  

void DFS(MGraph G, int v)
{
    visited[v]=true;
    cout<<G.vexs[v]<<" ";
    for(int w=FirstAdjVex(G, v); w>=0; w=NextAdjVex(G, v, w))
        if(!visited[w])
            DFS(G, w);
}  

void DFSTraverse(MGraph G)//深搜
{
    for(int i=0; i<G.vexnum; i++)
        visited[i]=false;  

    for(i=0; i<G.vexnum; i++)
        if(!visited[i])
            DFS(G, i);
}  

void BFSTraverse(MGraph G)//广搜,类似于树的层次遍历
{
    for(int i=0; i<G.vexnum; i++)
        visited[i]=false;  

    queue<int> q;  

    for(i=0; i<G.vexnum; i++)
    {
        if(!visited[i])
        {
            visited[i]=true;
            q.push(i);
            while(!q.empty())
            {
                int v=q.front();
                q.pop();
                cout<<G.vexs[v]<<" ";
                for(int w=FirstAdjVex(G, v); w>=0; w=NextAdjVex(G, v, w))
                {
                    if(!visited[w])
                    {
                        visited[w]=true;
                        q.push(w);
                    }
                }
            }
        }
    }
}  

void main()
{
    MGraph g;
    CreateUDG(g);  

    cout<<"深搜：";
    DFSTraverse(g);
    cout<<endl;  

    cout<<"广搜：";
    BFSTraverse(g);
    cout<<endl;
}  

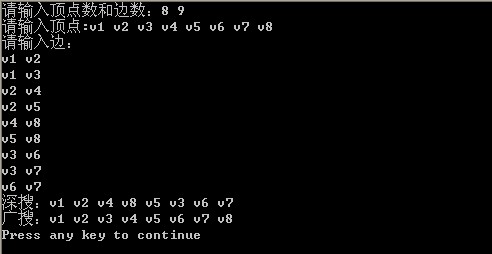
图的结构如下：