ALGO-27_蓝桥杯_算法训练_FBI树(树，递归)

问题描述
　　我们可以把由“”和“”组成的字符串分为三类：全“”串称为B串，全“”串称为I串，既含“”又含“”的串则称为F串。
　　FBI树是一种二叉树，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“”串S可以构造出一棵FBI树T，递归的构造方法如下：
　　)T的根结点为R，其类型与串S的类型相同；
　　)若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。
　　现在给定一个长度为2N的“”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历序列。
输入格式
　　第一行是一个整数N（ <= N <= ），第二行是一个长度为2N的“”串。
输出格式
　　包括一行，这一行只包含一个字符串，即FBI树的后序遍历序列。
样例输入

样例输出
IBFBBBFIBFIIIFF
数据规模和约定
　　对于40%的数据，N <= ；
　　对于全部的数据，N <= 。
　　注：
　　[] 二叉树：二叉树是结点的有限集合，这个集合或为空集，或由一个根结点和两棵不相交的二叉树组成。这两棵不相交的二叉树分别称为这个根结点的左子树和右子树。
　　[] 后序遍历：后序遍历是深度优先遍历二叉树的一种方法，它的递归定义是：先后序遍历左子树，再后序遍历右子树，最后访问根。

记:

一开始解题根据惯用FBI树解法：建树->递归判断数据并记录->后序输出树

　　　　　　　　

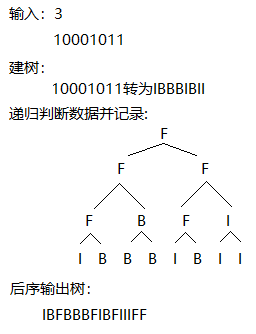
这种解法在输入n较大时会出现超时现象，

明显在建树以及后序输出遍历输出树的过程浪费了很多时间；

本题中的数据采用二叉树存储，而且是后序遍历输出树，

所以我们可以采用类似二分查找的形式，

先对输入数据进行二分区，然后进行判断

输出判断后的字符('F','B','I')，并返回

从而节省了建树以后序遍历输出树的时间。

AC代码:

 #include <stdio.h>
 #define MAX (1<<10)

 int n =  ;
 char str[MAX+] = {};

 void init()
 {
     int i,j;
     scanf("%d",&n);
     for (i =  ; i <= (<<n) ; i ++)
     {
         scanf("%1d",&j);
         /*将输入的数字串转换为FBI串*/
         if (j)
         {
             str[i] = 'I';
         }
         else
         {
             str[i] = 'B';
         }
     }
     return ;
 }

 char check(char l,char r)
 {
     if (l == 'B' && r == 'B')
     {
         return 'B';
     }
     else if (l == 'I' && r == 'I')
     {
         return 'I';
     }
     else
     {
         return 'F';
     }
 }

 char fbi(int x,int y)
 {
     int i = x , j = y , k = (y-x)/;
     char l,r,ans = str[i];
     if (i < j)
     {
         /*递归分区间*/
         l = fbi(i,i+k);/*左子树*/
         r = fbi(j-k,j);/*右子树*/
         ans = check(l,r);
     }
     printf("%c",ans);
     return ans;
 }

 int main(void)
 {
     init();
     fbi(,<<n);
     return ;
 }