NN中的激活函数【转载】
转自:https://blog.csdn.net/edogawachia/article/details/80043673
1.sigmoid
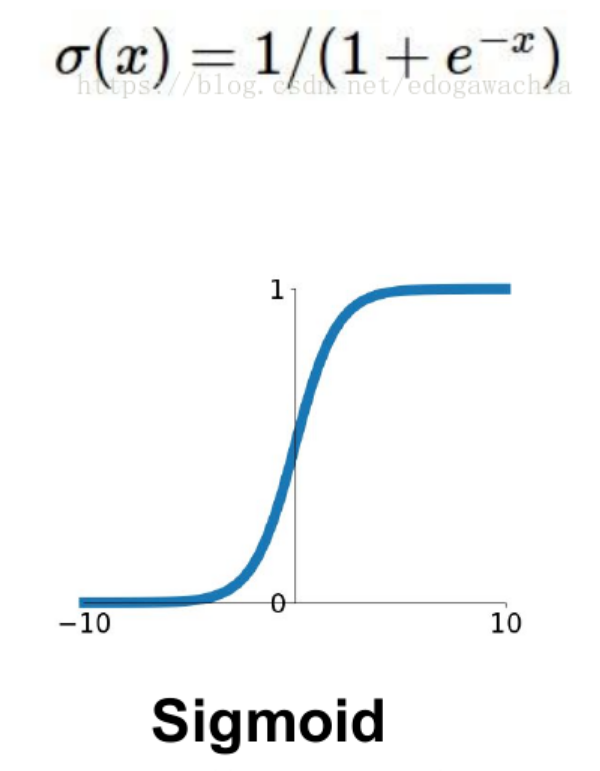
特点:可以解释,比如将0-1之间的取值解释成一个神经元的激活率(firing rate)
缺陷:
- 有饱和区域,是软饱和,在大的正数和负数作为输入的时候,梯度就会变成零,使得神经元基本不能更新。
- 只有正数输出(不是zero-centered,均值为0?),这就导致所谓的zigzag现象:

也就是说,w始终是朝着一直为正或者一直为负去变化的。

也就是说,更新只能朝着一个方向更新。
2.tanh函数
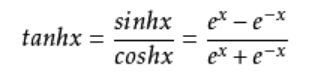
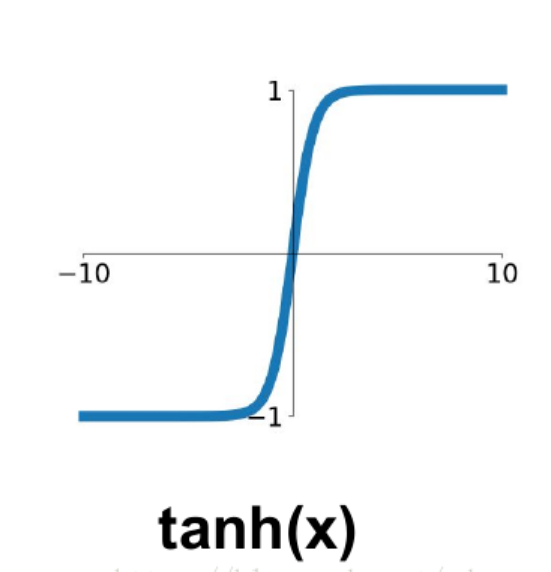
计算量大。
tanh和sigmoid函数是具有一定的关系的,可以从公式中看出,它们的形状是一样的,只是尺度和范围不同。
3.ReLU
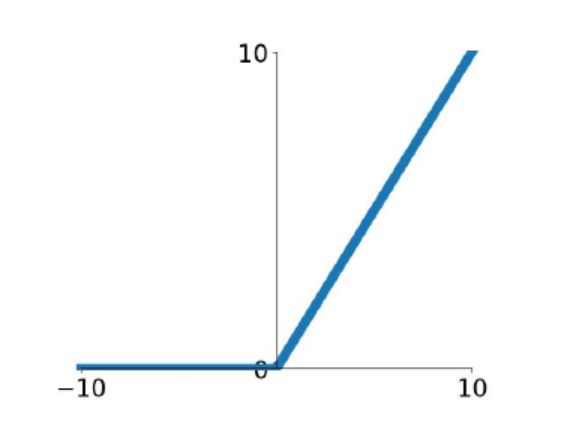
CNN中常用。对正数原样输出,负数直接置零。在正数不饱和,在负数硬饱和。relu计算上比sigmoid或者tanh更省计算量,因为不用exp,因而收敛较快。但是还是非zero-centered。
relu在负数区域被kill的现象叫做dead relu,这样的情况下,有人通过初始化的时候用一个稍微大于零的数比如0.01来初始化神经元,从而使得relu更偏向于激活而不是死掉,但是这个方法是否有效有争议。
4.LeakyReLU
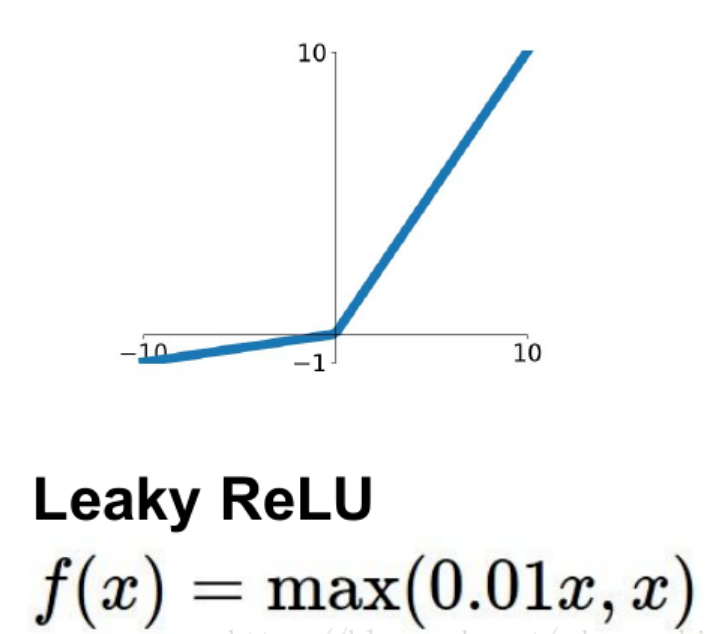
PReLU
parametric rectifier:
f(x) = max(ax,x)
但是这里的a不是固定下来的,而是可学习的。
ELU
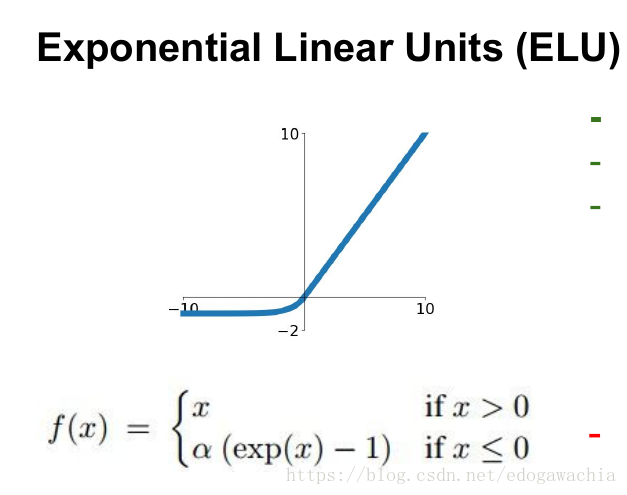
NN中的激活函数【转载】的更多相关文章
- 浅谈深度学习中的激活函数 - The Activation Function in Deep Learning
原文地址:http://www.cnblogs.com/rgvb178/p/6055213.html版权声明:本文为博主原创文章,未经博主允许不得转载. 激活函数的作用 首先,激活函数不是真的要去激活 ...
- The Activation Function in Deep Learning 浅谈深度学习中的激活函数
原文地址:http://www.cnblogs.com/rgvb178/p/6055213.html 版权声明:本文为博主原创文章,未经博主允许不得转载. 激活函数的作用 首先,激活函数不是真的要去激 ...
- 笔记+R︱信用风险建模中神经网络激活函数与感知器简述
每每以为攀得众山小,可.每每又切实来到起点,大牛们,缓缓脚步来俺笔记葩分享一下吧,please~ --------------------------- 本笔记源于CDA-DSC课程,由常国珍老师主讲 ...
- git在eclipse中的配置 转载
git在eclipse中的配置 转载 一_安装EGIT插件 http://download.eclipse.org/egit/updates/ 或者使用Eclipse Marketplace,搜索EG ...
- C#高级编程六十九天----DLR简介 .在.NET中使用DLR(转载) 我也来说说Dynamic
DLR 一.近年来,在TIOBE公司每个月发布的编程语言排行榜中,C#总是能挤进前十名,而在最近十年来,C#总体上呈现上升的趋势.C#能取得这样的成绩,有很多因素,其中它在语言特性上的锐意进取让人印象 ...
- C# json反序列化 对象中嵌套数组 (转载) 可能会导致循环或多重级联路径。请指定 ON DELETE NO ACTION 或 ON UPDATE NO ACTION,或修改其他 FOREIGN KEY 约束。
C# json反序列化 对象中嵌套数组 (转载) 看图: 这里可以看到是二层嵌套!!使用C#如何实现?? 思路:使用list集合实现 → 建立类 → list集合 → 微软的 Newtonso ...
- tensorflow中常用激活函数和损失函数
激活函数 各激活函数曲线对比 常用激活函数: tf.sigmoid() tf.tanh() tf.nn.relu() tf.nn.softplus() tf.nn.softmax() tf.nn.dr ...
- 神经网络中的激活函数——加入一些非线性的激活函数,整个网络中就引入了非线性部分,sigmoid 和 tanh作为激活函数的话,一定要注意一定要对 input 进行归一话,但是 ReLU 并不需要输入归一化
1 什么是激活函数? 激活函数,并不是去激活什么,而是指如何把“激活的神经元的特征”通过函数把特征保留并映射出来(保留特征,去除一些数据中是的冗余),这是神经网络能解决非线性问题关键. 目前知道的激活 ...
- Objective-C中的SEL (转载)
SEL 在Objective-C中,SEL是选择器(selector)的一个类型.选择器就是指向方法的一个指针,读者可以简单理解为程序运行到这里就会执行指定的方法,可以这样定义一个选择器: SEL ...
随机推荐
- ASP.NET MVC与ASP.NET Web Form简单区别
概论: Asp.net 微软 提供web开发框架或者技术.分Web Form和ASP.NET MVC.下面简单说明各自优缺点及使用场景. Web Form 优点: 1.支持丰富的服务器控件.如:Gr ...
- 正则表达式、re模块
正则表达式 一说规则我已经知道你很晕了,现在就让我们先来看一些实际的应用.在线测试工具 http://tool.chinaz.com/regex/ 正则表达式是用来匹配字符串非常强大的工具,在其他编程 ...
- [Android实例] Android Studio插件-自动根据布局生成Activity等代码1.4 (开源)(申明:来源于网络)
[Android实例] Android Studio插件-自动根据布局生成Activity等代码1.4 (开源)(申明:来源于网络) 地址:http://www.eoeandroid.com/thre ...
- Tarjan 强连通分量 及 双联通分量(求割点,割边)
Tarjan 强连通分量 及 双联通分量(求割点,割边) 众所周知,Tarjan的三大算法分别为 (1) 有向图的强联通分量 (2) 无向图的双联通分量(求割点,桥) ...
- QQ音乐flac音乐转MP6格式怎样实现
很多时候我们所下载的音乐格式都不是MP3格式的,用起来都是有局限性的,因为很多播放器都是支持MP3格式的.很多时候为了方便使用,我们就需要将不同的音乐格式转换为MP3格式的.如flac音乐转MP3的问 ...
- Error creating bean with name 'eurekaAutoServiceRegistration'
spring-boot项目不断重启,报错: org.springframework.beans.factory.BeanCreationNotAllowedException: Error creat ...
- {Python之线程} 一 背景知识 二 线程与进程的关系 三 线程的特点 四 线程的实际应用场景 五 内存中的线程 六 用户级线程和内核级线程(了解) 七 python与线程 八 Threading模块 九 锁 十 信号量 十一 事件Event 十二 条件Condition(了解) 十三 定时器
Python之线程 线程 本节目录 一 背景知识 二 线程与进程的关系 三 线程的特点 四 线程的实际应用场景 五 内存中的线程 六 用户级线程和内核级线程(了解) 七 python与线程 八 Thr ...
- distributed computing_the World Wide Web
RESTful Web APIs_2013 I'm going to show you a better way to do distributed computing, using the idea ...
- ldap,openldap-docker,
ldap basic and usage in devops: https://blog.csdn.net/weixin_42578481/article/details/80863890 maybe ...
- [development] __attribute__((weak))是干嘛的
简单的说,就是当发生 “重复定义的时候”.被声明者会被冲突者覆盖掉. 这里还涉及了weak与alias连用的情况. 参见,里边有两个例子,很浅显易懂. https://my.oschina.net/s ...
