BZOJ1845 [Cqoi2005] 三角形面积并 扫描线 计算几何

欢迎访问~原文出处——博客园-zhouzhendong

去博客园看该题解

---

题目传送门 - BZOJ1845

---

题意概括

　　给出n个三角形，求其面积并。

---

题解

　　有一个很经典的扫描线题目：矩形面积并。那个比较简单，建议先去看看 —— 传送门 - 矩形面积并。

　　这个扫描线的算法，我之前就看过。

　　之前想了想，还以为是n⁴logn的，自己以为理解错了，所以就弃坑了一段时间。

　　现在再想想，原来之前思考的是对的，只是复杂度想错了。其实是n³logn的。

　　我们按照Y来排序，同样的，我们来看一组图片。

　　

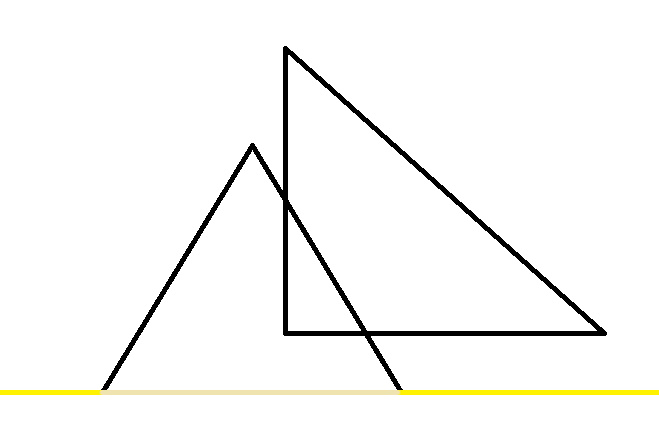
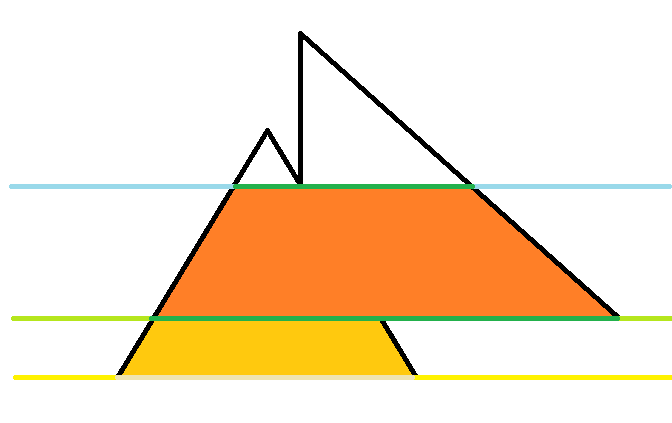
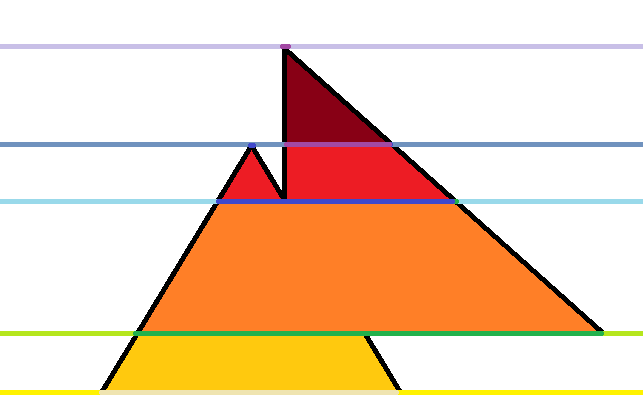
　　然后大概你已经深有感触了。

　　步骤：把所有的分成多个梯形，然后扫描线解决。

　　在这之前，我们需要把所有的交点都求出来。

　　当然，对于上例第一层和第二层的情况十分坑。第二条扫描线的有效长度不仅和其本身的参数有关，还和该边放在上面还是下面有关。

　　最后，诡异的是，ans要减去Eps才可以A掉。当然也有大佬不减的Orz，题目卡精度啊！

　　做个好人，代码后面一组数据。

---

代码

#include <cstring>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cmath>
using namespace std;
typedef long double LD;
const int N=300+5;
const LD Eps=1e-8,Inf=1e9;
int Dcmp(LD x){
	if (fabs(x)<Eps)
		return 0;
	return x<0?-1:1;
}
struct Point{
	LD x,y;
	Point (){}
	Point (LD x_,LD y_){
		x=x_,y=y_;
	}
	Point operator + (Point a){
		return Point(x+a.x,y+a.y);
	}
	Point operator - (Point a){
		return Point(x-a.x,y-a.y);
	}
	Point operator * (LD a){
		return Point(x*a,y*a);
	}
	Point operator / (LD a){
		return Point(x/a,y/a);
	}
	bool operator == (Point a){
		return !Dcmp(x-a.x)&&!Dcmp(y-a.y);
	}
	void read(){
		scanf("%Lf%Lf",&x,&y);
	}
};
LD Dot(Point a,Point b){
	return a.x*b.x+a.y*b.y;
}
LD Cross(Point a,Point b){
	return a.x*b.y-a.y*b.x;
}
LD Cross(Point a,Point b,Point c){
	return Cross(b-a,c-a);
}
struct Line{
	Point a,b;
	Line (){}
	Line (Point a_,Point b_){
		a=a_,b=b_;
	}
	Line Mat(){
		return Line(Point(min(a.x,b.x),min(a.y,b.y)),Point(max(a.x,b.x),max(a.y,b.y)));
	}
};
LD Length(Line a){
	return sqrt(Dot(a.a-a.b,a.a-a.b));
}
Point Cut_Point(Line L,LD y){
	Point a=L.a,b=L.b;
	LD da=y-a.y,dy=b.y-a.y,dx=b.x-a.x;
	if (!Dcmp(dy))
		return Point(Inf,Inf);
	return Point(a.x+dx/dy*da,y);
}
Line OrderedY_Line(Point a,Point b){
	if (Dcmp(a.x-b.x)>0)
		swap(a,b);
	return Line(a,b);
}
bool cmp_x(Point a,Point b){
	return Dcmp(a.x-b.x)<0;
}
bool cmp_y(Point a,Point b){
	return Dcmp(a.y-b.y)<0;
}
struct Triangle{
	Point P[3];
	Line L[3];
	void build(Point x,Point y,Point z){
		P[0]=x,P[1]=y,P[2]=z;
		L[0]=Line(x,y),L[1]=Line(x,z),L[2]=Line(y,z);
	}
	Line Cut(int type,LD Y,bool &flag){
		flag=1;
		Point P_[3];
		for (int i=0;i<3;i++)
			P_[i]=P[i];
		sort(P_,P_+3,cmp_y);
		if (Dcmp(P_[1].y-Y)==0&&Dcmp(P_[2].y-Y)==0)
			swap(P_[0],P_[2]);
		if (Dcmp(P_[0].y-Y)==0&&Dcmp(P_[1].y-Y)==0){
			if (type==0){
				if (Dcmp(P_[2].y-Y)<0){
					flag=0;
					return Line(Point(Inf,Inf),Point(Inf,Inf));
				}
				return OrderedY_Line(P_[0],P_[1]);
			}
			else {
				if (Dcmp(P_[2].y-Y)>0){
					flag=0;
					return Line(Point(Inf,Inf),Point(Inf,Inf));
				}
				return OrderedY_Line(P_[0],P_[1]);
			}
		}
		Point p[3];
		Line M[3];
		for (int i=0;i<3;i++){
			p[i]=Cut_Point(L[i],Y);
			M[i]=L[i].Mat();
		}
		if (Dcmp(Y-min(M[0].a.y,M[1].a.y))<0||Dcmp(Y-max(M[0].b.y,M[1].b.y))>0){
			flag=0;
			return Line(Point(Inf,Inf),Point(Inf,Inf));
		}
		for (int i=0;i<3;i++)
			if (Dcmp(Y-M[i].a.y)<0||Dcmp(Y-M[i].b.y)>0)
				return OrderedY_Line(p[(i+1)%3],p[(i+2)%3]);
		sort(p,p+3,cmp_x);
		return OrderedY_Line(p[0],p[0]==p[1]?p[2]:p[1]);
	}
};
bool Crossed(Line a,Line b){
	return Dcmp(Cross(a.a,a.b,b.a))*Dcmp(Cross(a.a,a.b,b.b))<0&&Dcmp(Cross(b.a,b.b,a.a))*Dcmp(Cross(b.a,b.b,a.b))<0;
}
Point Cross_Point(Line a,Line b){
	Point P=a.a,Q=b.a,v=a.b-a.a,w=b.b-b.a,u=P-Q;
	LD t=Cross(w,u)/Cross(v,w);
	return P+v*t;
}
int n,m;
Triangle Tri[N];
LD Y[N*N];
bool cmp_Lx(Line a,Line b){
	return Dcmp(a.a.x-b.a.x)<0;
}
LD GetLen(int type,int pos_Y){
	LD y=Y[pos_Y];
	Line L[N];
	int tot=0;
	for (int i=1;i<=n;i++){
		bool flag;
		L[++tot]=Tri[i].Cut(type,y,flag);
		if (!flag)
			tot--;
	}
	if (tot==0)
		return 0;
	sort(L+1,L+tot+1,cmp_Lx);
	LD ans=L[1].b.x-L[1].a.x,max_x=L[1].b.x;
	for (int i=2;i<=tot;i++){
		max_x=max(max_x,L[i].a.x);
		if (Dcmp(max_x-L[i].b.x)>0)
			continue;
		ans+=L[i].b.x-max_x;
		max_x=max(max_x,L[i].b.x);
	}
	return ans;
}
int main(){
	scanf("%d",&n);
	for (int i=1;i<=n;i++){
		Point x,y,z;
		x.read(),y.read(),z.read();
		Tri[i].build(x,y,z);
	}
	m=0;
	for (int i=1;i<=n;i++)
		for (int j=i+1;j<=n;j++)
			for (int u=0;u<3;u++)
				for (int v=0;v<3;v++)
					if (Crossed(Tri[i].L[u],Tri[j].L[v]))
						Y[++m]=Cross_Point(Tri[i].L[u],Tri[j].L[v]).y;
	for (int i=1;i<=n;i++)
		for (int j=0;j<3;j++)
			Y[++m]=Tri[i].P[j].y;
	sort(Y+1,Y+m+1);
	LD ans=0,pre=GetLen(0,1);
	for (int i=2;i<=m;i++){
		if (Dcmp(Y[i]-Y[i-1])==0)
			continue;
		ans+=0.5*(pre+GetLen(1,i))*(Y[i]-Y[i-1]);
		pre=GetLen(0,i);
	}
	printf("%.2Lf",ans-Eps);
	return 0;
}

　　

数据

2
0 0 2 0 0 3
2 0 0 2 3 2
ans=5.33

数据解释：