数据结构：二叉查找树(C语言实现)

数据结构：二叉查找树

二叉查找树

基础知识

　　关于二叉树的基础知识，请看我的一篇博客:二叉树的链式存储

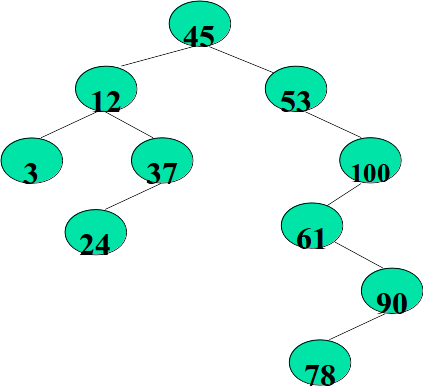
二叉查找树的特征

　　二叉查找树或者是一棵空树，或者是具有下列性质的二叉树：
　　1.若其左子树不空，则左子树上所有结点的值均小于它的根结点的值；
　　2.若其右子树不空，则右子树上所有结点的值均大于它的根结点的值;
　　3.其左、右子树也分别为二叉排序树

二叉查找树的建立

　　反复插入节点所构造出来的！若二叉树为空树，则插入元素作为树根节点。若根结点的键值等于key，则插入失败；若key小于根结点的键值，则插入到根的左子树上；否则，插入到根的右子树上新插入的节点一定是一个叶子节点！

代码分析

void InsertBST(BiStree &Tree,ElemType e)
{
    BiStree T =Tree;    //定义执行副本，！
    BiStree father =NULL; //定义
    while (T&&T->data.key!=e.key)
    {
        father=T;
        if(e.key>T->data.key)
            T=T->Rchild;
        else
            T=T->Lchild;
    }
    if(T) //跳出循环的只有两种情况，要么就是T不存在，要么就是找到了对应元素！T 存在说明，只能是对应元素也存在，那我我们就不用插入了
        return;
    BiSnode *s = (BiSnode*)malloc(sizeof(BiSnode));//能到这里，说明节点不存在，新建一个节点，并初始化！
    s->data=e;
    s->Rchild=s->Lchild=NULL;

    if(father==NULL)        //如果farther不存在，那说明就是没有执行While语句，也即是树是空的，因为一旦执行，就不会为NULL！
        Tree=s;
    else if(e.key>father->data.key) //到这里说明Farther存在,那么剩下的就是往farther左右节点插入元素了
        father->Rchild=s;
    else
        father->Lchild=s;
}

　　

删除运算

　　删除运算是的基础是查找元素，首先要查找要删除的元素，如果找到就删除，找不到就不用删除了。

查找代码

void DelBST(BiStree &Tree,char key)
{
    if(!Tree) //如果节点为空节点，说明要删除的元素不可能存在，所以返回就好！
        return;
    else //下面是节点存在的分情况判断：
    {
        if(Tree->data.key==key) //如果找到了要删除的节点！
        {
            deleteNode(Tree);   //删除该节点
        }
        else if(Tree->data.key<key)  //如果要删除的节点大于该节点，则往该节点的右子树方向进行查找
            DelBST(Tree->Rchild,key);
        else
            DelBST(Tree->Lchild,key);//如果要删除的节点小于该节点，则往该节点的左子树方向进行查找
    }
}

　　到现在我们已经找到元素了 ，要对其删除，就是要实现deleteNode(Tree);方法！
　　但是删除元素的运算是存在多种情况的，我们要分别处理：
　　　　★待删除的结点*p是个叶子结点

　　

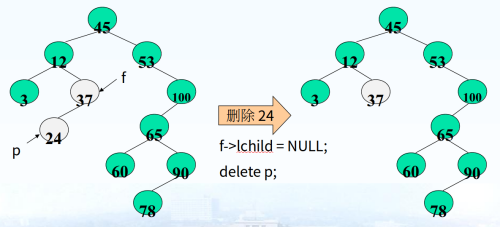
　　　　★待删除的结点*p是仅有一个非空子树

　　

　　　　★待删除的结点*p有两个非空子树

　　

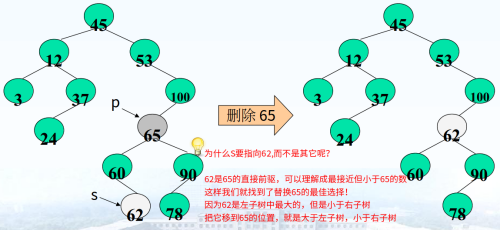
　　　　如何找出直接前驱:找到要删除节点的第一个左子树然后一直向右！ 　　

删除代码

void deleteNode(BiStree &p)
{
    if(!p->Rchild)  //对第一种及第二种情况的处理
    {
        BiSnode * q =p;
        p=p->Lchild;
        free(q);
    }
    else if(!p->Lchild) //对第一种及第二种情况的处理
    {
        BiSnode * q =p;
        p=p->Rchild;
        free(q);
    } else
    {
        BiSnode * q =p;
        BiSnode * s =p->Lchild;
        while (s->Rchild)
        {
            q=s;
            s=s->Rchild;
        }
        //s指向被删节点p的前驱
        p->data=s->data;
        if(q!=p) //详见下两图
            q->Rchild=s->Lchild;    //左图
         else
            q->Lchild=s->Lchild;    //右图
        free(s);
    }

}