hdu 1828 Picture(线段树 || 普通hash标记)

http://acm.hdu.edu.cn/showproblem.php?pid=1828

Picture

Time Limit: 6000/2000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 2135    Accepted Submission(s): 1134

Problem Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter.
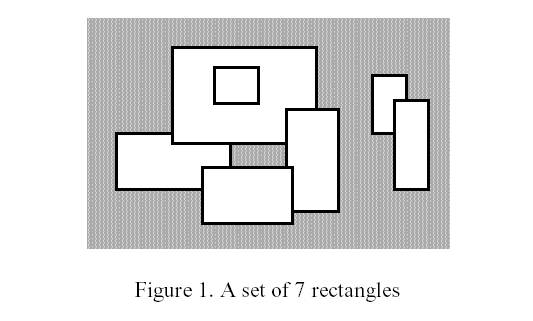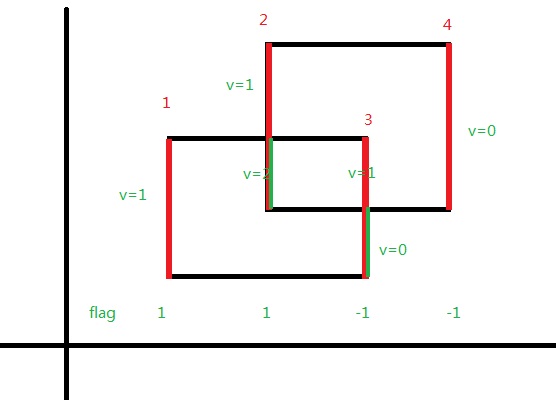
Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1.The corresponding boundary is the whole set of line segments drawn in Figure 2.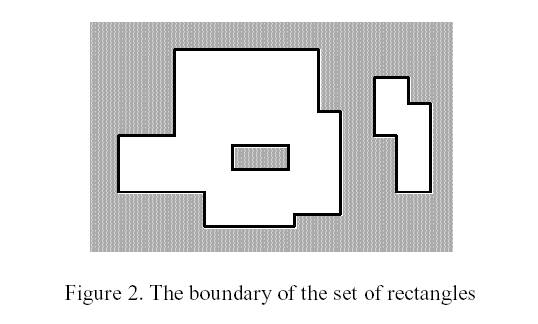The vertices of all rectangles have integer coordinates.

 

Input

Your program is to read from standard input. The first line contains the number of rectangles pasted on the wall. In each of the subsequent lines, one can find the integer coordinates of the lower left vertex and the upper right vertex of each rectangle. The values of those coordinates are given as ordered pairs consisting of an x-coordinate followed by a y-coordinate.
0 <= number of rectangles < 5000 All coordinates are in the range [-10000,10000] and any existing rectangle has a positive area.
Please process to the end of file.

 

Output

Your program is to write to standard output. The output must contain a single line with a non-negative integer which corresponds to the perimeter for the input rectangles.

 

Sample Input

7

-15 0 5 10

-5 8 20 25

15 -4 24 14

0 -6 16 4

2 15 10 22

30 10 36 20

34 0 40 16

 

Sample Output

228

 

Source

IOI 1998

 

【题解1】：

普通哈市标记：

分别按x,y方向用以下结构体构造线段：

struct Line
{
    int s,t;   //存始末位置
    int x;
    int flag;  //标记是否是起始边 1  -1
}linex[N<<1],liney[N<<1];  //分别安x与y构造线段

int visit[N<<2];  //判断是否访问过

再分别按x，y方向遍历标记

 

如下图：

按x方向的遍历线段1,2,3,4

 

【代码1】：

 #include <iostream>
 #include <string.h>
 #include <stdio.h>
 #include <algorithm>
 #define N 5010
 using namespace std;

 struct Line
 {
     int s,t;   //存始末位置
     int x;
     int flag;  //标记是否是起始边 1  -1
 }linex[N<<],liney[N<<];  //分别安x与y构造线段

 int visit[N<<];  //判断是否访问过

 bool cmp(Line a,Line b)  //sort排序用
 {
     return a.x<b.x;
 }

 int cal_x(int n)  //统计按x排序的平行于y的线段长
 {
     int i,j,cnt=;
     for(i=;i<=n;i++)
     {
         if(linex[i].flag == )  //如果是起始边
         {
             for(j=linex[i].s;j<linex[i].t;j++)
             {
                 if(visit[j]==) cnt++;  //起始边，没访问过cnt++
                 visit[j]++;  //标记+1
             }
         }
         else  //如果是结束边
         {
             for(j=linex[i].s;j<linex[i].t;j++)
             {
                 if(visit[j]==) cnt++;  //结束边，访问过cnt++
                 visit[j]--;  //标记-1，等待下一个起始边的进入
             }
         }
     }
     return cnt;
 }

 int cal_y(int n)  //同上，统计按y排序的平行于x的线段长
 {
     int i,j,cnt=;
     for(i=;i<=n;i++)
     {
         if(liney[i].flag == )
         {
             for(j=liney[i].s;j<liney[i].t;j++)
             {
                 if(visit[j]==) cnt++;
                 visit[j]++;
             }
         }
         else
         {
             for(j=liney[i].s;j<liney[i].t;j++)
             {
                 if(visit[j]==) cnt++;
                 visit[j]--;
             }
         }
     }
     return cnt;
 }

 int main()
 {
     int n;
     while(~scanf("%d",&n))
     {
         int i,cnt=;
         for(i=;i<n;i++)
         {
             int x1,y1,x2,y2;
             scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
             x1+=N<<;
             x2+=N<<;
             y1+=N<<;
             y2+=N<<;   //平移N<<1，排除负数情况

             cnt++;
             linex[cnt].x = x1;
             linex[cnt].s = y1;
             linex[cnt].t = y2;
             linex[cnt].flag = ;

             liney[cnt].x = y1;
             liney[cnt].s = x1;
             liney[cnt].t = x2;
             liney[cnt].flag = ;

             cnt++;
             linex[cnt].x = x2;
             linex[cnt].s = y1;
             linex[cnt].t = y2;
             linex[cnt].flag = -;

             liney[cnt].x = y2;
             liney[cnt].s = x1;
             liney[cnt].t = x2;
             liney[cnt].flag = -;
         }

         sort(linex+,linex++cnt,cmp);  //线段按x进行排序
         sort(liney+,liney++cnt,cmp);  //线段按y进行排序

         int ans = ;
         memset(visit,,sizeof(visit));
         ans += cal_x(cnt);  //统计x
         memset(visit,,sizeof(visit));
         ans += cal_y(cnt);  //统计y

         printf("%d\n",ans);
     }
     return ;
 }

【题解2】：线段树

线段树代码是参照别人的

【code】:

 #include<iostream>
 #include<string>
 #include<stdio.h>
 #include<algorithm>
 #include<cmath>
 using namespace std;

 struct node
 {
     int l;
     int r;
     int len;   //该区间可与下一个将要插入的线段组成并面积的长度
     int cover; //该区间覆盖了几根线段
     int num;   //记录该区间由几个子区间组成了可与下一个将要插入的线段组成并面积，即可并子区间的数目
     int r_cover; //记录该区间右节点是否被可并区间覆盖
     int l_cover; //。。。。。坐。。。。。。。。。
 };

 node tree[];
 int n;
 int yy[],len;

 struct Line
 {
     int l;
     int r;
     int x;
     int cover;
 };

 Line line[];

 int cmp(Line a,Line b)
 {
     return a.x<b.x;
 }

 int find(int x)
 {
     int l=,r=len,mid;
     while(l<=r)
     {
         mid=(l+r)/;
         if(yy[mid]==x)
             return mid;
         if(yy[mid]<x)
             l=mid+;
         else
             r=mid-;
     }
     return l;
 }

 void build(int i,int l,int r)
 {
     tree[i].l=l;
     tree[i].r=r;
     tree[i].cover=tree[i].l_cover=tree[i].r_cover=tree[i].len=tree[i].num=;
     if(l+==r)
         return;
     int mid=(l+r)/;
     build(*i,l,mid);
     build(*i+,mid,r);
 }

 void fun(int i)
 {
     if(tree[i].cover) //整个被覆盖
     {
         tree[i].len=yy[tree[i].r]-yy[tree[i].l]; //可用长度为整个区间
         tree[i].l_cover=tree[i].r_cover=; //左右节点都被覆盖了
         tree[i].num=;  //由一个区间组成，即该区间
     }
     else if(tree[i].l+==tree[i].r) //叶子区间
     {
         tree[i].len=;
         tree[i].l_cover=tree[i].r_cover=;
         tree[i].num=;
     }
     else
     {
         tree[i].len=tree[*i].len+tree[*i+].len; //dp
         tree[i].l_cover=tree[*i].l_cover; //左节点是否覆盖，取决于左子区间的左节点是否被覆盖
         tree[i].r_cover=tree[*i+].r_cover; //同理
         tree[i].num=tree[*i].num+tree[*i+].num-tree[*i].r_cover*tree[*i+].l_cover; //该线段可用长度的区间组成数等于左右子区间的组成数
     }                                                                                    //但是，当左右子区间是连续的时候，结果要减一
 }

 void updata(int i,int l,int r,int w)
 {
     if(tree[i].l>r || tree[i].r<l)
         return;
     if(tree[i].l>=l && tree[i].r<=r)
     {
         tree[i].cover+=w;
         fun(i);
         return;
     }
     updata(*i,l,r,w);
     updata(*i+,l,r,w);
     fun(i);
 }

 int main()
 {
     int i,x1,x2,y1,y2,m,a,b;
     //freopen("in.txt","r",stdin);
     while(scanf("%d",&n)!=EOF)
     {
         m=;
         for(i=;i<n;i++)
         {
             scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
             yy[m]=y1;
             line[m].cover=;
             line[m].x=x1;
             line[m].l=y1;
             line[m++].r=y2;

             yy[m]=y2;
             line[m].cover=-;
             line[m].x=x2;
             line[m].l=y1;
             line[m++].r=y2;
         }
         sort(yy,yy+m);
         sort(line,line+m,cmp);
         len=;
         for(i=;i<m;i++)  //?
         {
             if(yy[i-]!=yy[i])
                 yy[len++]=yy[i];
         }
         len--;
         build(,,len);
         int ans=,pre=;
         for(i=;i<m;i++)
         {
             a=find(line[i].l);
             b=find(line[i].r);
             updata(,a,b,line[i].cover);
             ans+=abs((tree[].len-pre)); //加上y坐标上的周长
             if(i==m-)
                 break;
             pre=tree[].len;
             ans+=tree[].num*(line[i+].x-line[i].x)*;//加上x坐标上的周长，因为一个y边连着两个x边，所以乘二
         }
         printf("%d\n",ans);
     }
     return ;
 }