DFSMN结构快速解读

参考文献如下：

(1) Deep Feed-Forward Sequential Memory Networks for Speech Synthesis

(2) Deep FSMN for Large Vocabulary Continuous Speech Recognition

1. cFSMN结构解析

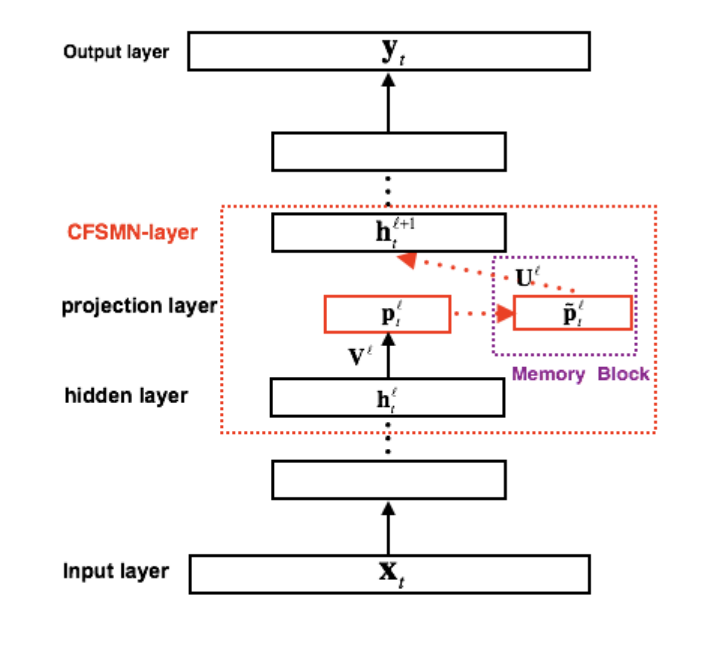
       有了之前对FSMN结构的了解，现在看cFSMN结构就很简单。由于FSMN需要将记忆模块的输出作为下一个隐层的额外输入，这样就会引入额外的模型参数。而隐层包含的节点越多，则引入的参数越多。

       基于此，cFSMN结合矩阵低秩分解的思路，通过在网络的隐层后添加一个低维度的线性投影层，并且将记忆模块添加在这些线性投影层上。进一步的，cFSMN对记忆模块的编码公式进行了一些改变，通过将当前时刻的输出显式的添加到记忆模块的表达中，从而只需要将记忆模块的表达作为下一层的输入。这样可以有效的减少模型的参数量，加快网络的训练。具体的，单向和双向的cFSMN记忆模块的公式表达分别如下：

\[
\vec{\tilde{p}_t^l} = \vec{p_t^l}+\sum_{i=0}^{N}\vec{a_i^l}\odot \vec{p_{t-i}^l}\tag{1}
\]

\[
\vec{\tilde{p}_t^l} = \vec{p_t^l}+\sum_{i=0}^{N_1}\vec{a_i^l}\odot\vec{p_{t-i}^l}+\sum_{j=0}^{N_2}\vec{c_j^l}\odot\vec{p_{t+j}^l}\tag{2}
\]

2.DFSMN结构解析

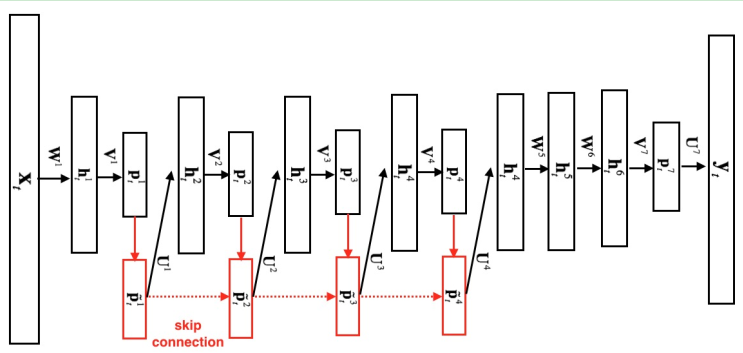
       观察结构图可以发现，DFSMN是在cFSMN的基础上，在不同层之间的记忆模块上添加了跳转链接skip connection，从而使得低层记忆模块的输出会被直接累加到高层记忆模块里。这样在训练过程中，高层记忆模块的梯度会直接赋值给低层的记忆模块，从而可以克服由于网络的深度造成的梯度消失问题，使得可以稳定地训练深层的网络。
       并且，通过借鉴扩张卷积的思路，DFSMN在记忆模块中引入了一些步幅因子stripe，具体的计算公式如下：

\[
\vec{\tilde{p}_t^l} = H(\vec{\tilde{p}_t^{l-1}})+\vec{p_t^l}+\sum_{i=0}^{N_1^l}\vec{a_i^l}\odot\vec{p_{t-{s_1*i}}^l}+\sum_{j=0}^{N_2^l}\vec{c_j^l}\odot\vec{p_{t+{s_2*j}}^l}\tag{3}
\]

       关于变换H可以是任意的线性或者非线性函数，特别的，如果每一层的记忆模块都是相同维度的，可以直接使用恒等映射：

\[
H(\vec{\tilde{p}_t^{l-1}}) = \vec{\tilde{p}_t^{l-1}}\tag{4}
\]

       至于为什么要引入步幅因子，是因为在实际工作处理中，临近单元信息会有大量的冗余，而步幅因子就可以帮助模型适当地消除这种冗余，从而加快模型的训练。