EZ 2018 05 20 NOIP2018 模拟赛（十五）

这次的比赛充满着玄学的气息，玄学链接

首先讲一下为什么没有第十四场

其实今天早上9点时看到题目就叫了：原题！

没错，整套试卷都做过，我还写了题解

然后老叶就说换一套，但如果仅仅是这样就没什么

但等13min后结束这场考试后，一评测发现有人A了T1

但老叶并没有开启Unrated，然后大家集体垫底被踩

然后我就莫名掉了74Rating

但是之后第二场很快就开始了，但是等第二场测完之后还是没有进行Unrated处理，结果就白掉分了

真是Dog至极

然后讲一下题目，这次主要是T2炸了，花了蛮长时间写O(n^2)的玄学的，然后所有数据点中竟没有一个点的n小于5000（全是90000+）

但是T3莫名快速幂多得了40pts还是很令人欣慰的

T1

这道题无疑是本场最不可做的一道题

具体的满分算法需要二维树状数组 or 主席树来搞

这里就直接优化一下暴力得50pts就很优秀了

由于本题数据n的范围不大，可以直接埃式筛来搞

50CODE

#include<cstdio>
using namespace std;
const int N=100005,MAX_SIZE=1000005;
int a[N],n,q,l[N],r[N],x[N],y[N],max_num;
bool prime[MAX_SIZE];
inline char tc(void)
{
	static char fl[100000],*A=fl,*B=fl;
	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0; char ch=tc();
	while (ch<'0'||ch>'9') ch=tc();
	while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc();
}
inline void write(long long x)
{
	if (x/10) write(x/10);
	putchar(x%10+'0');
}
inline int max(int a,int b)
{
	return a>b?a:b;
}
inline void get_prime(int m)
{
	register int i,j;
	for (prime[1]=1,i=2;i<=m;++i)
	if (!prime[i]) for (j=i<<1;j<=m;j+=i) prime[j]=1;
}
inline long long work(int l,int r,int x,int y)
{
	long long tot=0; register int i,j;
	for (i=x;i<=y;++i)
	if (!prime[i])
	for (j=l;j<=r;++j)
	{
		int now=a[j];
		while (!(now%i)) ++tot,now/=i;
	}
	return tot;
}
int main()
{
	//freopen("A.in","r",stdin); freopen("A.out","w",stdout);
	register int i;
	for (read(n),i=1;i<=n;++i)
	read(a[i]);
	for (read(q),i=1;i<=q;++i)
	read(l[i]),read(r[i]),read(x[i]),read(y[i]),max_num=max(max_num,y[i]);
	get_prime(max_num);
	for (i=1;i<=q;++i)
	write(work(l[i],r[i],x[i],y[i])),putchar('\n');
	return 0;
}

T2

这其实时一道比较经典的水题了

我们先考虑在一条直线上的情况，就是Luogu P1367

假设两只蚂蚁A，B面对面相遇：

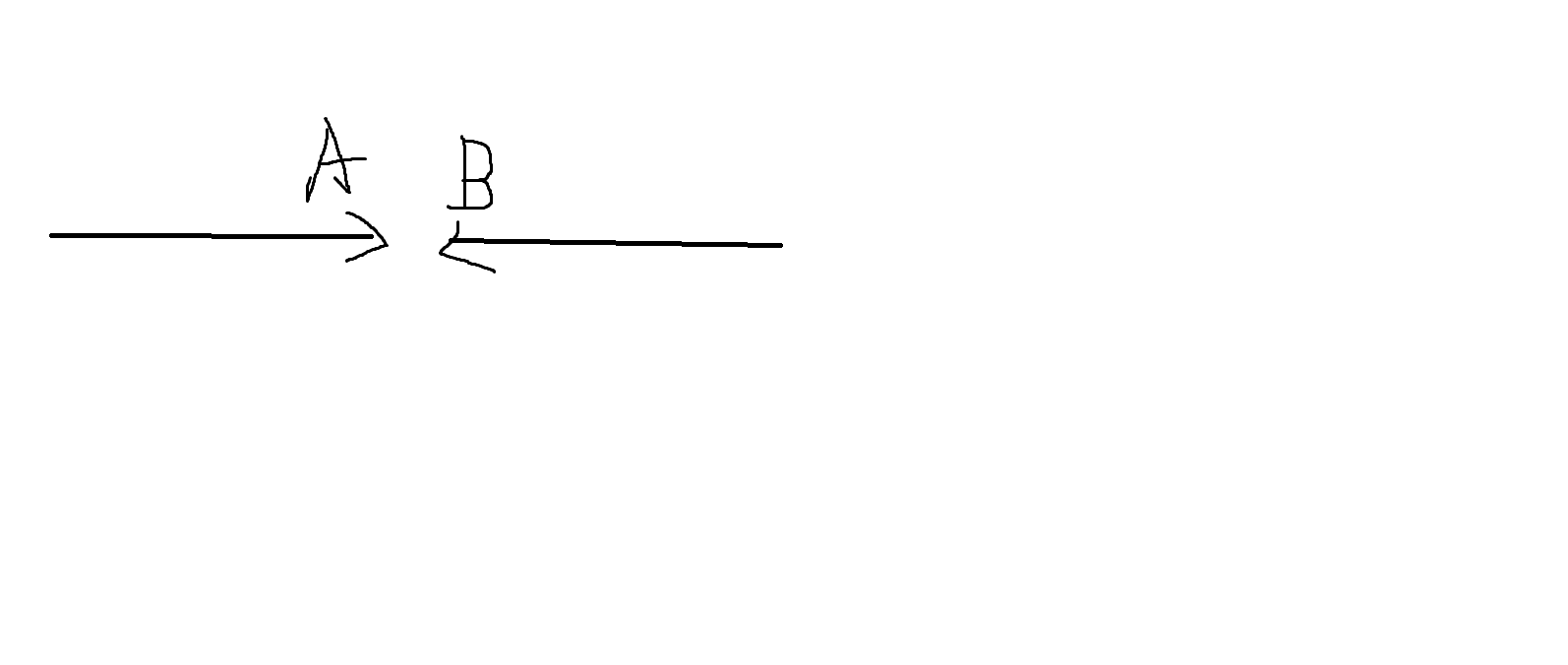
然后他们掉头，相当于穿过了对方并且互换身份：

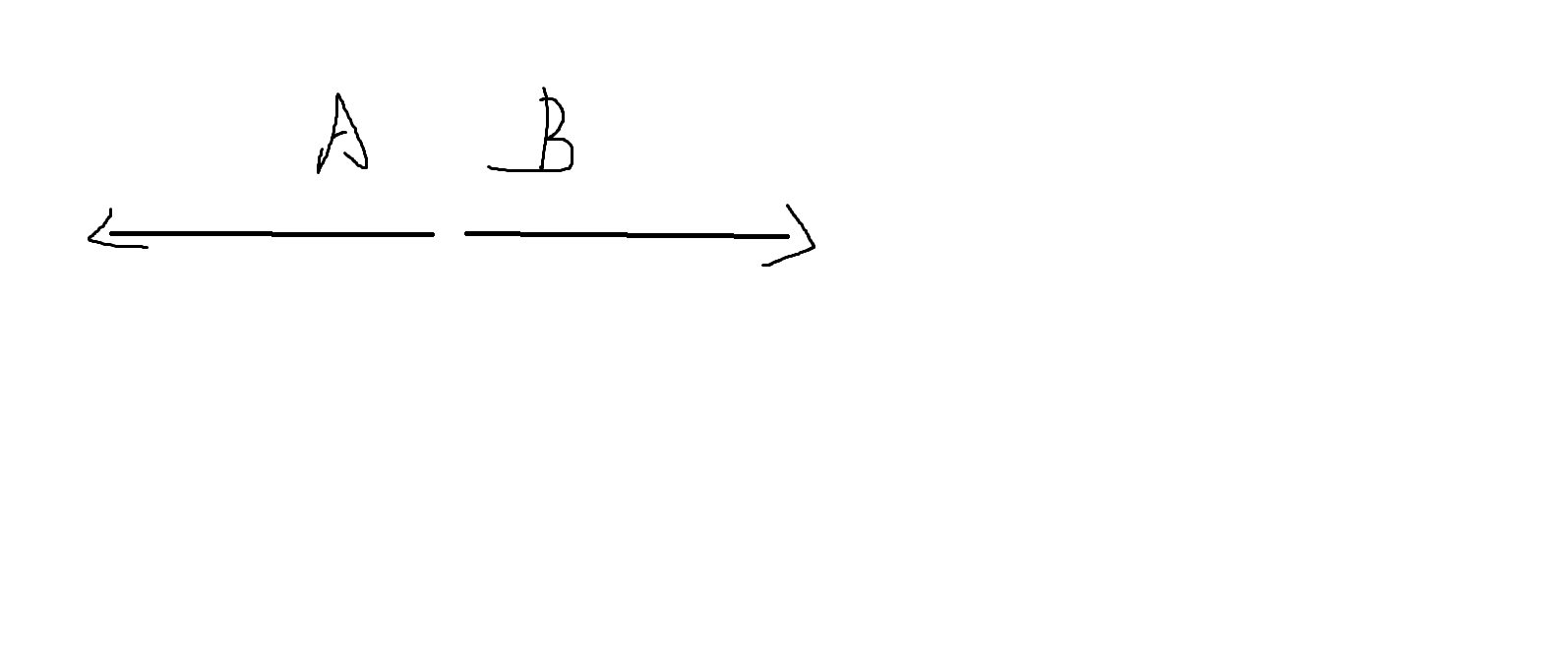
但是有一个性质：它们的相对位置不会改变

什么意思——就是不管它们怎么移动，第i只蚂蚁的左边一定是第i-1只蚂蚁，右边一定是第i+1只蚂蚁

然后只要sort一下就可以了

但是对于这道题是一个圆的情况，则有些在后面的蚂蚁可能会排到前面去

但是蚂蚁的位置还是不变，并且相对位置保持相对不变，因此我们只要知道第1只蚂蚁的位置就可以顺次求出后面蚂蚁的位置

我们设第一只蚂蚁的相对排名为cnt，初始值为1.每当一只蚂蚁从l-1到达0时，cnt++；每当一只蚂蚁从0爬到l-1时，cnt--

然后就排序后通过cnt正确输出顺序即可

因为当前HHHOJ没有开放这次题目，因此到Atcoder提交即可

CODE

#include<cstdio>
#include<algorithm>
const int N=1e5+5;
int a[N],n,l,t,x,w;
long long cnt=1;
using namespace std;
inline char tc(void)
{
	static char fl[100000],*A=fl,*B=fl;
	return A==B&&(B=(A=fl)+fread(fl,1,100000,stdin),A==B)?EOF:*A++;
}
inline void read(int &x)
{
	x=0; char ch=tc();
	while (ch<'0'||ch>'9') ch=tc();
	while (ch>='0'&&ch<='9') x=x*10+ch-'0',ch=tc();
}
inline void write(int x)
{
	if (x/10) write(x/10);
	putchar(x%10+'0');
}
int main()
{
	//freopen("B.in","r",stdin); freopen("B.out","w",stdout);
	register int i;
	read(n); read(l); read(t);
	for (i=1;i<=n;++i)
	{
		read(x); read(w);
		if (w==1) a[i]=(x+t)%l,cnt+=(x+t)/l; else a[i]=(x-t%l+l)%l,cnt-=t%l>x?t/l+1:t/l;
	}
	cnt=(cnt%n+n-1)%n+1;
	sort(a+1,a+n+1);
	for (i=cnt;i<=n;++i)
	write(a[i]),putchar('\n');
	for (i=1;i<cnt;++i)
	write(a[i]),putchar('\n');
	return 0;
}

T3

首先30pts的爆搜不讲

然后这题有一个性质：若n>=m，即ans为2^2m，因为就有所有的塔都有可能红或蓝

快速幂求之即可，结合爆搜可以得70pts

考虑DP，这里用r表示红的，b表示蓝的

我们首先发现，每一次操作的时候加上去的要么是"rr","rb","br","bb"，而且手上红色蓝色的和总是为n

而且条件很简单，若第一位r则此时手上必须有1个r

然后我们设f[i][j]表示进行第i次操作时手上有j个红色的方案总数，则蓝的有n-j个

又发现这样可能会用重复的方案，然后我们发现：若对于两种状态，手上的红色个数不为0，那么它们就重复了

因此我们设f[i][j][0/1]表示此时红色的是否取完过，然后再转移即可

Atcoder链接

CODE

#include<cstdio>
#include<cstring>
using namespace std;
const int N=3005,mod=1e9+7;
int f[2][N][2],n,m,ans;
inline void inc(int &x,int y)
{
	x+=y; x-=x>=mod?mod:0;
}
int main()
{
	register int i,j,k;
	scanf("%d%d",&n,&m);
	for (i=1;i<=n;++i)
	f[0][i][0]=1; f[0][0][1]=1;
	for (i=0;i<m;++i)
	{
		int now=i&1,nxt=now^1;
		memset(f[nxt],0,sizeof(f[nxt]));
		for (j=0;j<=n;++j)
		for (k=0;k<=1;++k)
		{
			if (j) inc(f[nxt][j-1][k|(j==1)],f[now][j][k]);
			if (j) inc(f[nxt][j][k|(j==1)],f[now][j][k]);
			if (n-j) inc(f[nxt][j+1][k],f[now][j][k]);
			if (n-j) inc(f[nxt][j][k],f[now][j][k]);
		}
	}
	for (i=0;i<=n;++i)
	inc(ans,f[m&1][i][1]);
	printf("%d",ans);
	return 0;
}