【CF542D】Superhero's Job 暴力

【CF542D】Superhero's Job

题意：$ f(x)=\sum\limits_{d|x,gcd(d,{x\over d})=1} d$

给出 $A$ ，求方程 $f(x)=A$ 的正整数解的个数。

$1\le A\le 10^{12}$

题解：首先我们发现f这个函数是积性的，$f(p^a)=1+p^a$（p是质数）。所以我们枚举$A$的所有约数，看一下他能不能拆成$1+p^a$的形式，并把p相同的放到一起。设f[i]表示乘积为i的方案数，暴力DP即可。你甚至可以用map。

附：$10^{12}$以内约数最多的数为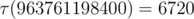

#include <cstring>
#include <iostream>
#include <cstdio>
#include <map>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N=1000000;

ll n;
int num,m,cnt,tot,tim;
int ep[100];
int pri[N>>1],np[N+10],f[2][10000];

ll v[10000],pr[100];
struct node
{
	int bel;
	ll val;
}p[10000];
map<ll,int> ref,vis;
void dfs(int x,ll now)
{
	if(x==m+1)
	{
		v[++tot]=now,ref[now]=tot;
		return ;
	}
	for(int i=0;i<=ep[x];i++)	dfs(x+1,now),now*=pr[x];
}
bool cmp(const node &a,const node &b)
{
	return (a.bel==b.bel)?(a.val<b.val):(a.bel<b.bel);
}
int main()
{
	scanf("%lld",&n);
	int i,j,d=0;
	ll tn=sqrt(n);
	for(i=2;i<=tn;i++)
	{
		if(!np[i])	pri[++num]=i;
		for(j=1;j<=num&&i*pri[j]<=tn;j++)
		{
			np[i*pri[j]]=1;
			if(i%pri[j]==0)	break;
		}
	}
	ll t=n;
	for(i=1;i<=num&&pri[i]*pri[i]<=t;i++)	if(t%pri[i]==0)
	{
		pr[++m]=pri[i];
		while(t%pri[i]==0)	t/=pri[i],ep[m]++;
	}
	if(t!=1)	pr[++m]=t,ep[m]=1;
	dfs(1,1);
	for(i=2;i<=tot;i++)	if(v[i]!=2)
	{
		t=v[i]-1;
		int flag=1;
		for(j=1;j<=num&&pri[j]*pri[j]<=t;j++)	if(t%pri[j]==0)
		{
			t/=pri[j];
			while(t%pri[j]==0)	t/=pri[j];
			if(t!=1)	flag=0;
			else	t=pri[j];
			break;
		}
		if(flag)
		{
			p[++cnt].val=v[i];
			if(!vis[t])	vis[t]=++tim;
			p[cnt].bel=vis[t];
		}
	}
	sort(p+1,p+cnt+1,cmp);
	f[0][1]=1;
	for(j=1;j<=cnt;j++)
	{
		if(p[j].bel!=p[j-1].bel)	d^=1,memcpy(f[d],f[d^1],sizeof(f[0][0])*(tot+1));
		for(i=1;i<=tot;i++)	if(v[i]%p[j].val==0)
			f[d][i]+=f[d^1][ref[v[i]/p[j].val]];
	}
	printf("%d",f[d][tot]);
	return 0;
}