bc38 1002, bc39 1002

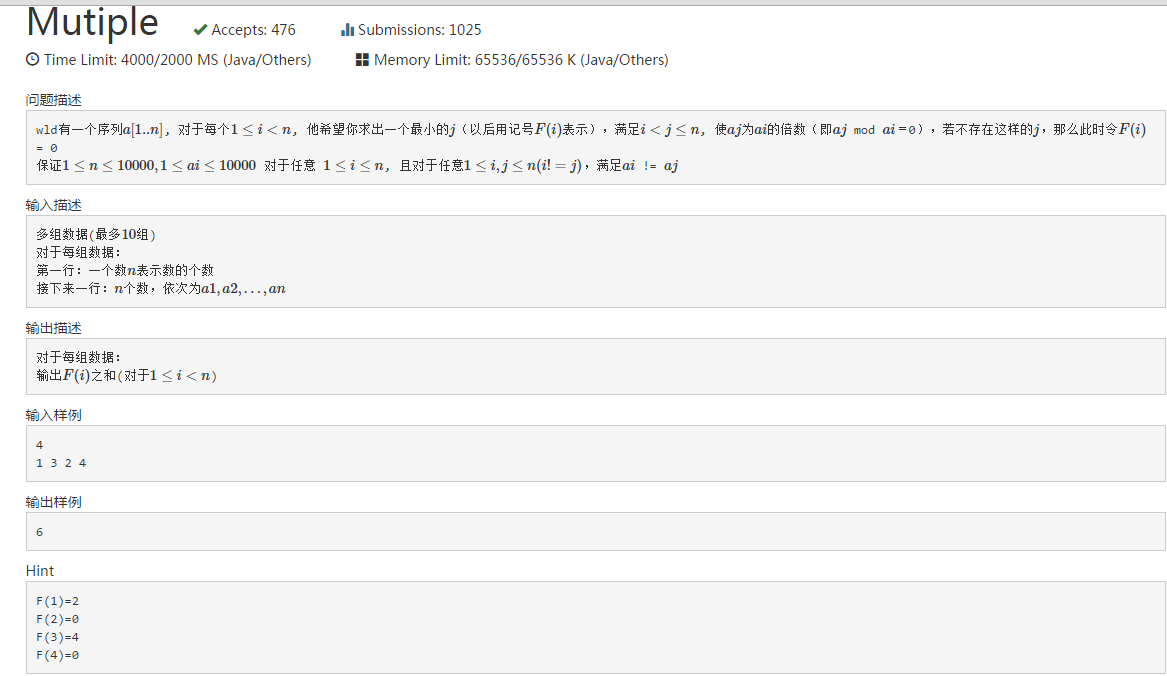
比赛的时候是对于每个数，记录下来a[i]， 并记录该树的下标hash[a[i]]

然后枚举a[i]的倍数，如果a[i]的倍数存在(设为k*a[i])，那么vis[k*a[i]]是不为0的

那么可以这样枚举得到最小的下标，但是比赛的时候不懂算时间复杂度，就随便提交了一下，没想到过了。

后来看了下题解，原来时间复杂度是这样算的

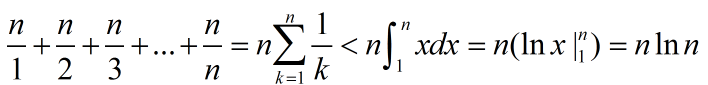
 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <algorithm>
 #include <iostream>
 #include <queue>
 #include <stack>
 #include <vector>
 #include <map>
 #include <set>
 #include <string>
 #include <math.h>
 using namespace std;
 #pragma warning(disable:4996)
 typedef long long LL;
 const int INF = <<;
 /*

 */
 const int N =  + ;
 int vis[N];
 int a[N];
 int main()
 {
     int n, i, ans,j;
     while (scanf("%d", &n) != EOF)
     {
         memset(vis, , sizeof(vis));
         for (i = ; i <= n; ++i)
         {
             scanf("%d", &a[i]);
             vis[a[i]] = i;
         }
         ans = ;
         for (i = ; i <= n; ++i)
         {
             bool find = false;
             int index;
             for (j = ; j*a[i] <= ; ++j)
             {
                 int v = j * a[i];
                 //找到最小的下标
                 if (!vis[v])
                     continue;
                 if (vis[v] < i)
                     continue;
                 if (!find)
                 {
                     index = vis[v];
                     find = true;
                 }
                 else
                     index = min(index, vis[v]);

             }
             if (find)
                 ans += index;
         }
         printf("%d\n", ans);
     }
     return ;
 }

然后想起bc38场的第2题好像也是类似这样子。

我可以hash每个数，即hash[a[i]]++

然后从大到小枚举约数，然后再枚举约数的倍数，如果出现过两次约数的倍数，那么该约数就是最大的约数。 需要注意的是因为a[i]可能重复，所以hash[a[i]]++

这题的时间复杂度和上面一样，也是O(nlgn)

 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <algorithm>
 #include <iostream>
 #include <queue>
 #include <stack>
 #include <vector>
 #include <map>
 #include <set>
 #include <string>
 #include <math.h>
 using namespace std;
 #pragma warning(disable:4996)
 typedef long long LL;
 const int INF = <<;
 /*

 */
 const int N =  + ;
 int a[N];
 int vis[N];
 int main()
 {
     int t, n, i, k;
     int ans,Max;
     scanf("%d", &t);
     for (k = ; k <= t; ++k)
     {
         Max = -;
         scanf("%d", &n);
         memset(vis, , sizeof(vis));
         for (i = ; i < n; ++i)
         {
             scanf("%d", &a[i]);
             Max = max(Max, a[i]);
             vis[a[i]] ++;
         }
         for (i = Max; i >= ; --i)//枚举约数
         {
             int flag = ;
             for (int j = ; j*i <= Max; ++j)//枚举约数的倍数，
             {
                 int v = j * i;
                 flag += vis[v];
                 if (flag >=)
                     break;
             }
             if (flag >= )
                 break;
         }
         printf("Case #%d: %d\n", k, i);
     }
     return ;
 }