洛谷—— P2668 斗地主

https://www.luogu.org/problem/show?pid=2668

题目描述

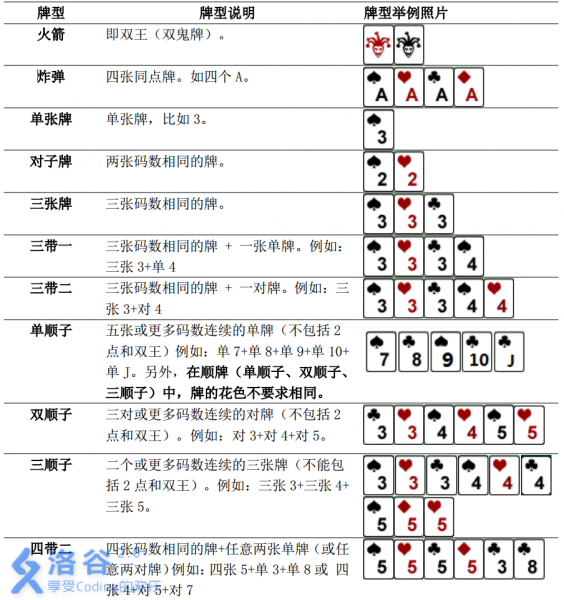
牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由n张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。

具体规则如下：

本题数据随机，不支持hack，要hack或强力数据请点击这里

输入输出格式

输入格式：

第一行包含用空格隔开的2个正整数T和n，表示手牌的组数以及每组手牌的张数。

接下来T组数据，每组数据n行，每行一个非负整数对aibi表示一张牌，其中ai示牌的数码，bi表示牌的花色，中间用空格隔开。特别的，我们用1来表示数码A，11表示数码J，12表示数码Q，13表示数码K；黑桃、红心、梅花、方片分别用1-4来表示；小王的表示方法为01，大王的表示方法为02。

输出格式：

共T行，每行一个整数，表示打光第i手牌的最少次数。

输入输出样例

输入样例#1：

输出样例#1：

输入样例#2：

输出样例#2：

说明

样例1说明

共有1组手牌，包含8张牌：方片7，方片8，黑桃9，方片10，黑桃J，黑桃5，方片A以及黑桃A。可以通过打单顺子（方片7，方片8，黑桃9，方片10，黑桃J），单张牌（黑桃5）以及对子牌（黑桃A以及方片A）在3次内打光。

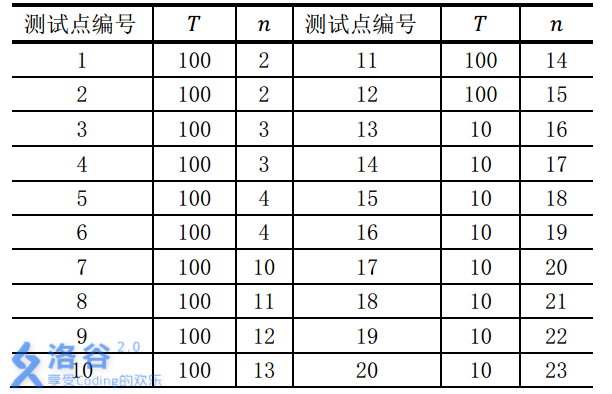
对于不同的测试点，我们约定手牌组数T与张数n的规模如下：

数据保证：所有的手牌都是随机生成的。

DFS每次出的顺子情况，带牌及单出的牌暴力得出步数、

 #include <cstring>

 #include <cstdio>

 int n,tot[],tmp[],ans;

 inline void read(int &x)

 {

     x=; register char ch=getchar();

     for(;ch>''||ch<'';) ch=getchar();

     for(;ch>=''&&ch<='';ch=getchar()) x=x*+ch-'';

 }

 int Sum()

 {

     int card=;                //card表示带牌用的步数

     memset(tmp,,sizeof(tmp));

     for(int i=; i<=; ++i) tmp[tot[i]]++;

     for(; tmp[]&&tmp[]>; ) tmp[]--,tmp[]-=,card++;    //四带两个对牌

     for(; tmp[]&&tmp[]>; ) tmp[]--,tmp[]-=,card++;    //四带两个异花单牌

     for(; tmp[]&&tmp[]; ) tmp[]--,tmp[]--,card++;        //四带两个同花单排

     for(; tmp[]&&tmp[]; ) tmp[]--,tmp[]--,card++;        //三带一

     for(; tmp[]&&tmp[]; ) tmp[]--,tmp[]--,card++;        //三代二

     return card+tmp[]+tmp[]+tmp[]+tmp[];        //带牌步数+剩余需要单出的牌

 }

 void DFS(int cnt)

 {

     if(cnt>=ans) return ;

     int add=Sum();

     ans=ans<(cnt+add)?ans:(cnt+add); 

     for(int i=; i<=; ++i)    //三顺子

     {

         int j=i;

         for(; tot[j]>; ) j++;

         if(j-i<) continue;

         for(int t=i+; t<j; t++)

         {

             for(int k=i; k<=t; k++) tot[k]-=;

             DFS(cnt+);

             for(int k=i; k<=t; k++) tot[k]+=;

         }

     }

     for(int i=; i<=; ++i)    //双顺子

     {

         int j=i;

         for(; tot[j]>; ) j++;

         if(j-i<) continue;

         for(int t=i+; t<j; t++)

         {

             for(int k=i; k<=t; k++) tot[k]-=;

             DFS(cnt+);

             for(int k=i; k<=t; k++) tot[k]+=;

         }

     }

     for(int i=; i<=; ++i)    //单顺子

     {

         int j=i;

         for(; tot[j]; ) j++;

         if(j-i<) continue;

         for(int t=i+; t<j; t++)

         {

             for(int k=i; k<=t; k++) tot[k]--;

             DFS(cnt+);

             for(int k=i; k<=t; k++) tot[k]++;

         }

     }

 }

 int Hope()

 {

 //    freopen("my.txt","w",stdout);

     int t; read(t),read(n);

     for(int col,x; t--; )

     {

         ans=0x3f3f3f3f;

         memset(tot,,sizeof(tot));

         for(int i=; i<=n; ++i)

         {

             scanf("%d%d",&x,&col);

             if(x==) x=;

             else if(!x) x=;

             tot[x]++;

         }

         DFS();

         printf("%d\n",ans);

     }

     return ;

 }

 int Aptal=Hope();

 int main(){;}