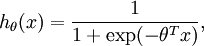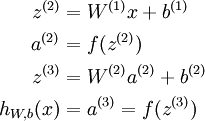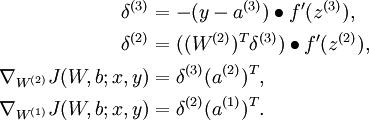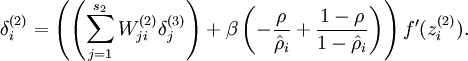Vectorized implementation

Vectorization

Vectorization refers to a powerful way to speed up your algorithms. Numerical computing and parallel computing researchers have put decades of work into making certain numerical operations (such as matrix-matrix multiplication, matrix-matrix addition, matrix-vector multiplication) fast. The idea of vectorization is that we would like to express our learning algorithms in terms of these highly optimized operations.

More generally, a good rule-of-thumb for coding Matlab/Octave is:

Whenever possible, avoid using explicit for-loops in your code.

A large part of vectorizing our Matlab/Octave code will focus on getting rid of for loops, since this lets Matlab/Octave extract more parallelism from your code, while also incurring less computational overhead from the interpreter.

多用向量运算，别把向量拆成标量然后再循环

Logistic Regression Vectorization Example

Consider training a logistic regression model using batch gradient ascent. Suppose our hypothesis is

where we let , so that and , and is our intercept term. We have a training set of examples, and the batch gradient ascent update rule is , where is the log likelihood and is its derivative.

We thus need to compute the gradient:

Further, suppose the Matlab/Octave variable y is a row vector of the labels in the training set, so that the variable y(i) is .

Here's truly horrible, extremely slow, implementation of the gradient computation:

% Implementation
grad = zeros(n+,);
for i=:m,
  h = sigmoid(theta'*x(:,i));
  temp = y(i) - h;
  for j=:n+,
    grad(j) = grad(j) + temp * x(j,i);
  end;
end;

The two nested for-loops makes this very slow. Here's a more typical implementation, that partially vectorizes the algorithm and gets better performance:

% Implementation
grad = zeros(n+,);
for i=:m,
  grad = grad + (y(i) - sigmoid(theta'*x(:,i)))* x(:,i);
end;

Neural Network Vectorization

Forward propagation

Consider a 3 layer neural network (with one input, one hidden, and one output layer), and suppose x is a column vector containing a single training example . Then the forward propagation step is given by:

This is a fairly efficient implementation for a single example. If we have m examples, then we would wrap a for loop around this.

% Unvectorized implementation
for i=:m,
  z2 = W1 * x(:,i) + b1;
  a2 = f(z2);
  z3 = W2 * a2 + b2;
  h(:,i) = f(z3);
end;

For many algorithms, we will represent intermediate stages of computation via vectors. For example, z2, a2, and z3 here are all column vectors that're used to compute the activations of the hidden and output layers. In order to take better advantage of parallelism and efficient matrix operations, we would like to have our algorithm operate simultaneously on many training examples. Let us temporarily ignore b1 and b2 (say, set them to zero for now). We can then implement the following:

% Vectorized implementation (ignoring b1, b2)
z2 = W1 * x;
a2 = f(z2);
z3 = W2 * a2;
h = f(z3)

In this implementation, z2, a2, and z3 are all matrices, with one column per training example.

A common design pattern in vectorizing across training examples is that whereas previously we had a column vector (such as z2) per training example, we can often instead try to compute a matrix so that all of these column vectors are stacked together to form a matrix. Concretely, in this example, a2 becomes a s₂ by m matrix (where s₂ is the number of units in layer 2 of the network, and m is the number of training examples). And, the i-th column of a2 contains the activations of the hidden units (layer 2 of the network) when the i-th training example x(:,i) is input to the network.

% Inefficient, unvectorized implementation of the activation function
function output = unvectorized_f(z)
output = zeros(size(z))
for i=:size(z,),
  for j=:size(z,),
    output(i,j) = /(+exp(-z(i,j)));
  end;
end;
end

% Efficient, vectorized implementation of the activation function
function output = vectorized_f(z)
output = ./(+exp(-z));     % "./" is Matlab/Octave's element-wise division operator.
end

Finally, our vectorized implementation of forward propagation above had ignored b1 and b2. To incorporate those back in, we will use Matlab/Octave's built-in repmat function. We have:

% Vectorized implementation of forward propagation
z2 = W1 * x + repmat(b1,,m);
a2 = f(z2);
z3 = W2 * a2 + repmat(b2,,m);
h = f(z3)

repmat ！！矩阵变形！！

Backpropagation

We are in a supervised learning setting, so that we have a training set of m training examples. (For the autoencoder, we simply set y⁽ⁱ⁾ = x⁽ⁱ⁾, but our derivation here will consider this more general setting.)

we had that for a single training example (x,y), we can compute the derivatives as

Here, denotes element-wise product. For simplicity, our description here will ignore the derivatives with respect to b^(l), though your implementation of backpropagation will have to compute those derivatives too.

gradW1 = zeros(size(W1));
gradW2 = zeros(size(W2));
for i=:m,
  delta3 = -(y(:,i) - h(:,i)) .* fprime(z3(:,i));
  delta2 = W2'*delta3(:,i) .* fprime(z2(:,i));

  gradW2 = gradW2 + delta3*a2(:,i)';
  gradW1 = gradW1 + delta2*a1(:,i)';
end;

This implementation has a for loop. We would like to come up with an implementation that simultaneously performs backpropagation on all the examples, and eliminates this for loop.

To do so, we will replace the vectors delta3 and delta2 with matrices, where one column of each matrix corresponds to each training example. We will also implement a function fprime(z) that takes as input a matrix z, and applies element-wise.

Sparse autoencoder

When performing backpropagation on a single training example, we had taken into the account the sparsity penalty by computing the following:

也就是不要用循环一个样本一个样本的去更新参数，而是要将样本组织成矩阵的形式，应用矩阵运算，提高效率。