wireshark抓包蓝色和红色

在默认情况下

蓝色适合红色相反的方向

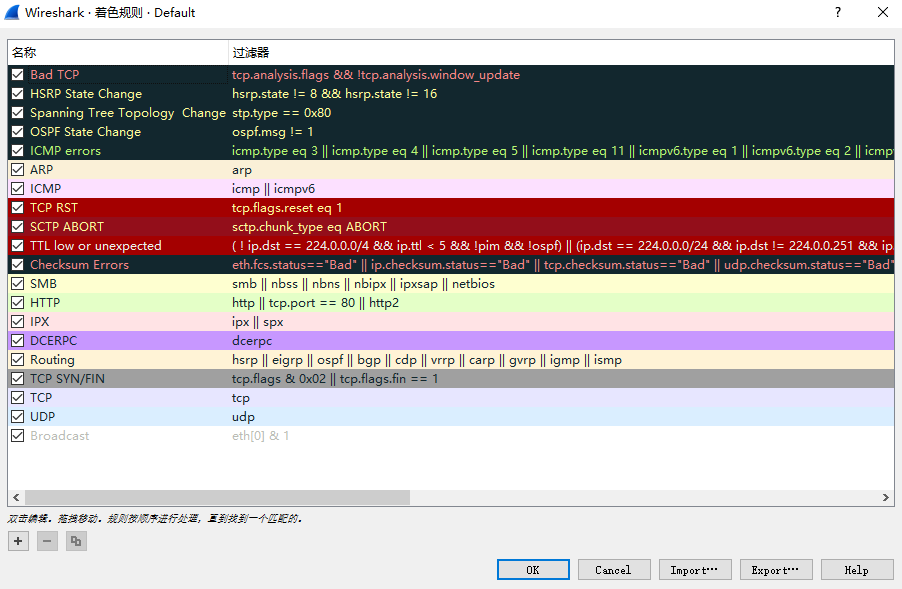
绿色背景的是HTTP包
灰色背景的是TCP包。
黑色背景的是TCP错误包或者校验和错误的包

有时候wireshark抓的包还有颜色区分，想知道为什么吗？

如果汉化：

视图->着色规则

如果未汉化：

view->coloring rules

嘎嘎嘎嘎嘎过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过过

Wireshark着色规则的更多相关文章

  1. Wireshark网络抓包(一)——数据包、着色规则和提示

    一.数据包详细信息 Packet Details面板内容如下,主要用于分析封包的详细信息. 帧:物理层.链路层 包:网络层 段:传输层.应用层 1)Frame 物理层数据帧概况 2)Ethernet ...

  2. 【汇总】Wireshark 过滤规则

    作者:Bay0net 时间:2019-07-01 14:20:09 更新: 介绍:记录使用过的 wireshark 过滤规则 0x01. 使用介绍 抓包采用 wireshark,提取特征时,要对 se ...

  3. 【转】wireshark过滤规则

    WireShark过滤语法 1.过滤IP,如来源IP或者目标IP等于某个IP 例子:ip.src eq 192.168.1.107 or ip.dst eq 192.168.1.107或者ip.add ...

  4. wireshark过滤规则

    WireShark过滤语法 1.过 滤IP,如来源IP或者目标IP等于某个IP 例子:ip.src eq 192.168.1.107 or ip.dst eq 192.168.1.107或者ip.ad ...

  5. 【转】WireShark 过滤规则

    原链:[渗透神器系列]WireShark wireshark是一款网络流量抓取分析神器,也是安全工具使用排行中排名第一的工具.使用wireshark必须要牢记一些常用的数据包过滤规则,对于寻找一些特定 ...

  6. 转： wireshark过滤规则

    转: http://blog.sina.com.cn/s/blog_48a0f2740100ka71.html WireShark过滤语法 1.过 滤IP,如来源IP或者目标IP等于某个IP 例子: ...

  7. Wireshark - 过滤规则

    使用 Wireshark 的默认设置抓包时,会得到大量的冗余信息,以至于很难找到自己所需的封包.使用过滤器可以帮助我们在庞杂的结果中快速地找到我们所需的封包.过滤器分为两种:捕捉过滤器和显示过滤器. ...

  8. 【HTTP】Wireshark过滤规则

    参考:http://jingyan.baidu.com/article/454316ab593170f7a6c03a60.html 语句特点:协议.属性 一.IP过滤: 包括来源IP或者目标IP等于某 ...

  9. 干货，Wireshark使用技巧-过滤规则

    - 过滤规则使用 在抓取报文时使用的规则,称为过滤规则,Wireshark底层是基于Winpcap,因此过滤规则是Winpcap定义的规则,设置过滤规则后,抓到的报文仅包含符合规则的报文,其它报文则被 ...

随机推荐

  1. wed前端html/css简单理解

    开发工具: txt文本 / dreamwave:DW(cs6/cc) / Hbuilder / webstorm / sublime / vscode 前端: 知识架构: 3层: 结构 / 表现 / ...

  2. Ansible常用模块介绍

    ansible < HOST-PATTERN > [ -f FORKS ] [ -m MOUDULE ] [ -a "ARGS" ] [ -o ] MOUDULE: p ...

  3. Markdown教程 <1>

    Markdown教程 <1> 本文在本地使用atom编辑后,直接将代码赋值到博客园中的markdown编辑器中生成 1. markdown字体,段落控制 以下引用块里面为源码,引用块下方为 ...

  4. Spring源码阅读-IoC容器解析

    目录 Spring IoC容器 ApplicationContext设计解析 BeanFactory ListableBeanFactory HierarchicalBeanFactory Messa ...

  5. 全自动Landsat影像温度反演软件开发

    许久没有更新遥感类软件开发了,都有点生疏了,这一次我带来了一个老的算法,新的东西, 为什么这么说呢,我们知道Landat8.Landsat5等影像,单个影像去做温度反演,并没有什么太大的难度, 但是呢 ...

  6. angular安装

    安装时间:20190703安装环境:win10 1 安装Nodejs 1.1 下载地址:https://nodejs.org/en/ 1.2 下载完成之后双击安装,安装完成之后无需配置环境变量(安装的 ...

  7. string类总结第二部分实战练习

    第二部门:实战练习 昨天由于时间原因,这个部分应该在同一个文章中的,无奈只能今天再开一个了,今天主要是讲一些面试题 一:equals和==的区别 最简单的面试题,也是最基础的,我估计每个学习java的 ...

  8. Java学习笔记——三层架构

    Layer: UI层: user interface 用户接口层 Biz层:   service business login layer 业务逻辑层 DAO层:   Date Access Obje ...

  9. Codeforces Round #564 (Div. 2)A

    A. Nauuo and Votes 题目链接:http://codeforces.com/contest/1173/problem/A 题目 Nauuo is a girl who loves wr ...

  10. JVM史上最全实践优化没有之一

    JVM史上最全优化没有之一 1.jvm的运行参数 1.1 三种参数类型 1.1.1 -server与-clinet参数 2.1 -X参数 2.1.1 -Xint.-Xcomp.-Xmixed 3.1 ...