Largest Rectangle in a Histogram POJ - 2559 （单调栈）

Description

A histogram is a polygon composed of a sequence of rectangles aligned at a common base line. The rectangles have equal widths but may have different heights. For example, the figure on the left shows the histogram that consists of rectangles with the heights 2, 1, 4, 5, 1, 3, 3, measured in units where 1 is the width of the rectangles:


Usually, histograms are used to represent discrete distributions, e.g., the frequencies of characters in texts. Note that the order of the rectangles, i.e., their heights, is important. Calculate the area of the largest rectangle in a histogram that is aligned at the common base line, too. The figure on the right shows the largest aligned rectangle for the depicted histogram.

Input

The input contains several test cases. Each test case describes a histogram and starts with an integer n, denoting the number of rectangles it is composed of. You may assume that 1<=n<=100000. Then follow n integers h₁,...,h_n, where 0<=h_i<=1000000000. These numbers denote the heights of the rectangles of the histogram in left-to-right order. The width of each rectangle is 1. A zero follows the input for the last test case.

Output

For each test case output on a single line the area of the largest rectangle in the specified histogram. Remember that this rectangle must be aligned at the common base line.

Sample Input

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

Sample Output

8
4000

Hint

Huge input, scanf is recommended.

 

题意：n个矩形，然后给出每个矩形的高（宽度都为1），求出其中最大矩形的面积

 

思路：对于高度递增的矩形序列，我们可以尝试以每一块的高度为最终高度，然后向后延申宽度，最大面积就是答案。

但是当前高度小于之前矩形的高度时，我们可以先回溯，之前的矩形肯定时高度递增的，回溯的目的时更新之前矩形所能形成的最大的答案

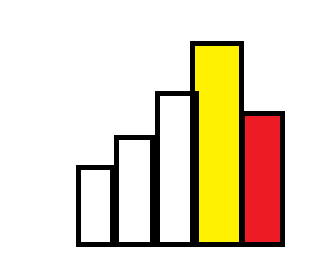
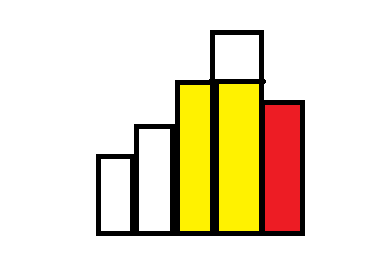
（黄色区域为回溯时，矩形高度仍大于当前矩形，更新的答案）

 

直到之前的矩形高度小于当前矩形，就将之前所积累的（宽度+1），当成新矩形的宽度，高度就是当前矩形高度，这样的对于后面的矩形，又形成了新的递增型矩形序列

而且由于回溯的时候，我们将舍弃的部分能形成的最大面积已经考虑了，所以不会出现答案遗失（对于后面的矩形紫色无法利用的，被当前矩形限制了高度，所以舍弃，加入扩展了的当前矩形）

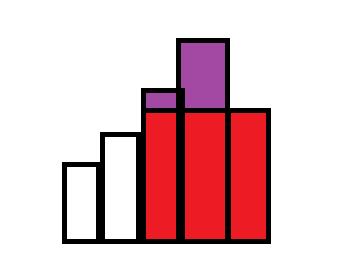
最后，对整个递增的矩形序列进行一次回溯，答案的更新，为了方便将其最后加入一个高度为0的矩形，当然不加另外判断也ok

（用不用栈无所谓，重要的是单调性）

#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;

typedef long long ll;
const int maxn = 1e5+;
stack<ll>s;
ll ans;
int w[maxn];
int h[maxn];
int n;
int main()
{
    while(~scanf("%d",&n) && n)
    {
        for(int i=;i<=n;i++)scanf("%d",&h[i]);
        while(!s.empty())s.pop();
        int pos = ;
        h[n+] = ;
        ans = ;
        for(int i=;i<=n+;i++)
        {
            if(s.empty() || h[i] >= s.top())
            {
                s.push(h[i]);
                w[++pos] = ;
            }
            else
            {
                int width = ;
                while(!s.empty() && s.top() > h[i])
                {
                    width += w[pos];
                    ans = max(ans,s.top()*width);
                    s.pop();
                    pos--;
                }
                s.push(h[i]);
                w[++pos] = width+;
            }
        }
        printf("%lld\n",ans);
    }
}