SLAM的数学基础(2):协方差和协方差矩阵
之前我们知道,方差是一组数据的离散程度,它的公式为:

那么如果我们有几组数据,需要知道这几组数据的协同性呢?
举个例子,还是在小红,几次考试成绩如下:
入学考试:数学:80,语文:80
期中考试:数学:90,语文:70
期末考试:数学:70,语文:90
小蓝,几次考试成绩如下:
入学考试:数学:60,语文:60
期中考试:数学:70,语文:70
期末考试:数学:80,语文:80
好,我们把数据放着,先说一下概念。所谓的协方差,就是用来统计两组数据之间的协同程度,协方差矩阵是用来遍历不同组数据的方差。
协方差用公式表示为:
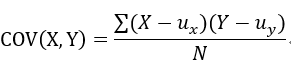
方差是协方差的特殊表现形式,即X=Y的时候。
OK,我们现在再来看上面的数据,根据这个公式,计算小红数学和总分的协方差为:
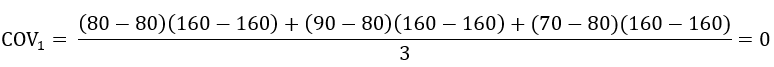
计算小蓝数学和总分的协方差为:

从这些数据上可以看出,小红的协方差为0,表明数学和总分没有什么关系,因为他的数学考得好,语文就考的不好。但小蓝的协方差是正的,表示他的数学进步,语文也跟着进步,总分自然提高了,是个全面发展的好青年。
那么我们想全面的表现语文、数学、总分之间的相关性,该如何表示呢?嗯,有个东西叫协方差矩阵,它可以表示多组数据之间两两之间的协方差。

比如按上面小红的数学成绩和总分的关系,形成数据集
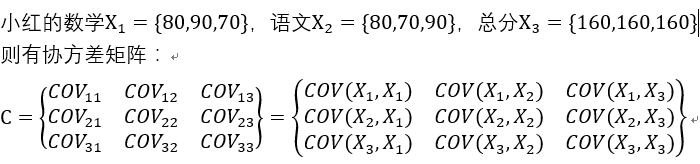
SLAM的数学基础(2):协方差和协方差矩阵的更多相关文章
- 方差variance, 协方差covariance, 协方差矩阵covariance matrix
https://www.jianshu.com/p/e1c8270477bc?utm_campaign=maleskine&utm_content=note&utm_medium=se ...
- 方差variance, 协方差covariance, 协方差矩阵covariance matrix | scatter matrix | weighted covariance | Eigenvalues and eigenvectors
covariance, co本能的想到双变量,用于描述两个变量之间的关系. correlation,相关性,covariance标准化后就是correlation. covariance的定义: 期望 ...
- 视觉SLAM的数学基础 第一篇 3D空间的位置表示
视觉SLAM中的数学基础 第一篇 3D空间的位置表示 前言 转眼间一个学期又将过去,距离我上次写<一起做RGBD SLAM>已经半年之久.<一起做>系列反响很不错,主要由于它为 ...
- SLAM的数学基础(4):先验概率、后验概率、贝叶斯准则
假设有事件A和事件B,可以同时发生但不是完全同时发生,如以下韦恩图所示: 其中,A∩B表示A和B的并集,即A和B同时发生的概率. 如此,我们很容易得出,在事件B发生的情况下,事件A发生的概率为: 这个 ...
- SLAM的数学基础(3):几种常见的概率分布的实现及验证。
分布,在计算机学科里一般是指概率分布,是概率论的基本概念之一.分布反映的是随机或某个系统中的某个变量,它的取值的范围和规律. 常见的分布有:二项分布.泊松分布.正态分布.指数分布等,下面对它们进行一一 ...
- SLAM的数学基础(1):什么是方差,有什么意义?
小红班上有两组同学的数学考试分数为: 第一组:小红:100分,小明:60分,小宇:20分 第二组:小蓝:70分,小华:60分,小杰:50分 那么很容易算出,第一组的平均分是60分,第二组的平均分也是6 ...
- 自主移动机器人同时定位与地图创建(SLAM)方法概述
1.引言: 机器人的研究越来越多的得到关注和投入,随着计算机技术和人工智能的发展,智能自主移动机器人成为机器人领域的一个重要研究方向和研究热点.移动机器人的定位和地图创建是自主移动机器人领域的热点研究 ...
- 协方差(Covariance)
统计学上用方差和标准差来度量数据的离散程度 ,但是方差和标准差是用来描述一维数据的(或者说是多维数据的一个维度),现实生活中我们常常会碰到多维数据,因此人们发明了协方差(covariance),用来度 ...
- 向量的表示及协方差矩阵 (PCA的理论基础)
原文:http://blog.csdn.net/songzitea/article/details/18219237 引言 当面对的数据被抽象为一组向量,那么有必要研究一些向量的数学性质.而这些数学性 ...
随机推荐
- TensorFlow用法
TensorFlow用法 什么是TensorFlow TensorFlow是一个开源软件库,用于使用数据流图进行数值计算.图中的节点表示数学运算,而图的边缘表示流动的多维数据数组(张量).这种灵活的体 ...
- Minkowski坐标管理
Minkowski坐标管理 坐标键 classMinkowskiEngine.CoordsKey(D) __init__(D) 初始化self. See help(type(self))有关准确的签名 ...
- Linux内存技术分析(下)
Linux内存技术分析(下) 五.内存使用场景 out of memory 的时代过去了吗?no,内存再充足也不可任性使用. 1.内存的使用场景 page 管理 slab(kmalloc.内存池) 用 ...
- 适用于Windows和Linux的Yolo-v3和Yolo-v2(上)
适用于Windows和Linux的Yolo-v3和Yolo-v2(上) https://github.com/eric-erki/darknetAB (用于对象检测的神经网络)-Tensor Core ...
- Class.forName()、Class.forName().newInstance() 、New 三者区别!
终于明白为什么加载数据库驱动只用Class.forName()了!!困扰了我2个小时!!希望我写的这个东西对各位有所帮助. 在Java开发特别是数据库开发中,经常会用到Class.forNa ...
- kube-proxy IPVS 模式的工作原理
原文链接:https://fuckcloudnative.io/posts/ipvs-how-kubernetes-services-direct-traffic-to-pods/ Kubernete ...
- 【NX二次开发】 获取体的面 UF_MODL_ask_body_faces
获取体的面 1 extern DllExport void ufsta(char *param, int *returnCode, int rlen) 2 { 3 UF_initialize(); 4 ...
- VBS脚本编程(4)——流程控制语句
分支结构--If .. Then .. Else .. 根据表达式的值有条件地执行一组语句. If condition Then statements [Else elsestatements ] 或 ...
- Android开发万能Utils(工具大全)
AndroidUtils Android开发不得不收藏的Utils About AndroidUtilCode 是一个强大易用的安卓工具类库,它合理地封装了安卓开发中常用的函数,具有完善的 Demo ...
- 最强阿里巴巴历年经典面试题汇总:C++研发岗
(1).B树.存储模型 (2).字典树构造及其优化与应用 (3).持久化数据结构,序列化与反序列化时机(4).在无序数组中找最大的K个数? (4).大规模文本文件,全是单词,求前10词频的单词 (5) ...
