CF80B Depression 题解

Content

有一个时针，给定时间为 \(\text{HH}\) 时 \(\text{MM}\) 分，求图中 \(\alpha\) 和 \(\beta\) 角的值。

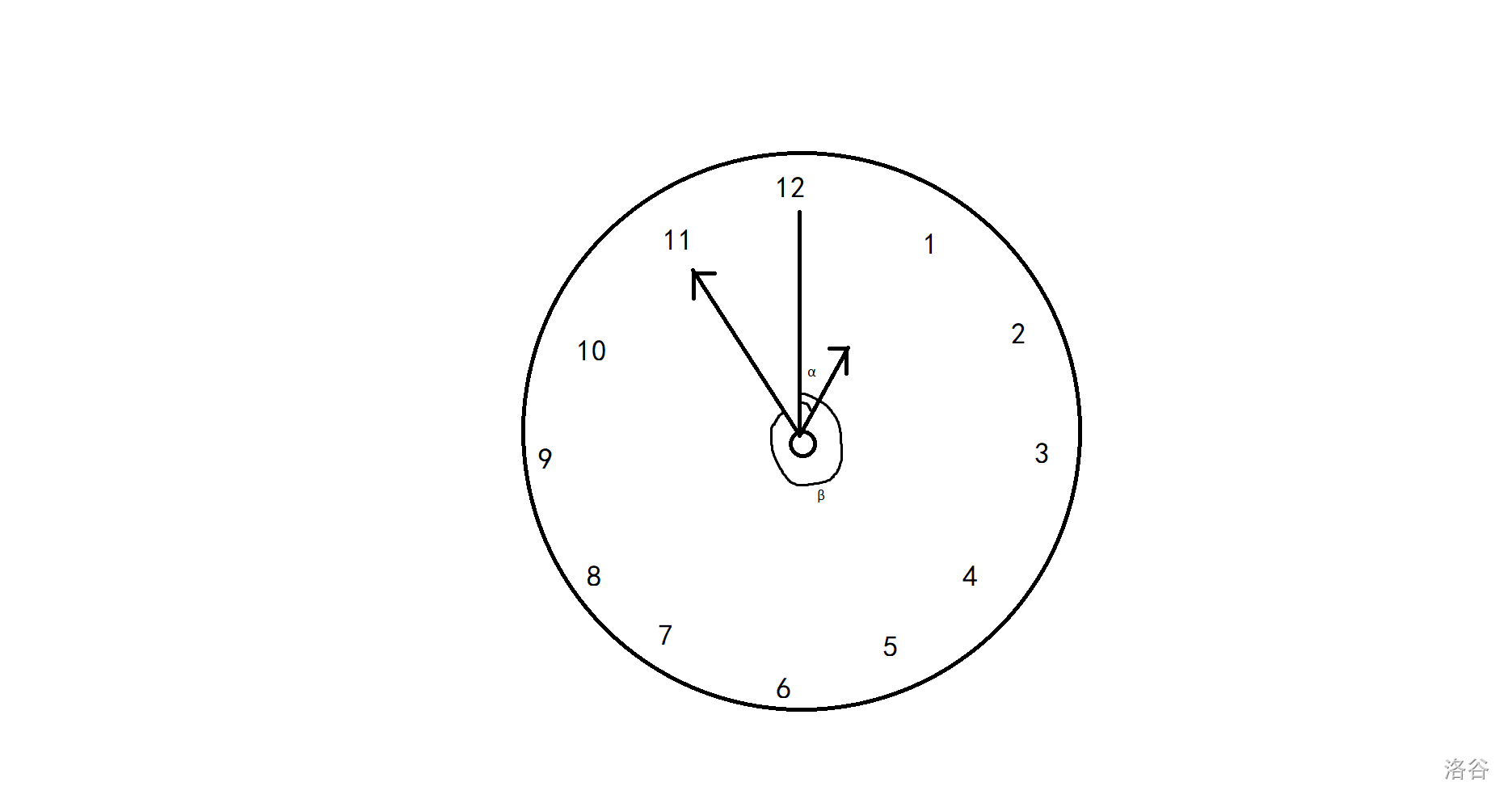
手画勿喷/kk

数据范围：\(0\leqslant\text{HH}\leqslant23,0\leqslant\text{MM}\leqslant59\)。

Solution

答案很明显可以手推出来。

首先，小时数 \(\geqslant12\) 的要减去 \(12\)，因为这样才是对于时钟上面显示的样子。不过在代码中也可以用 \(\text{HH}\leftarrow\text{HH}\mod12\) 来表示。

又我们知道，一小时内，时针转 \(30\) 度，一分钟内，时针转 \(0.5\) 度，分针转 \(6\) 度。

所以，答案就是 \(30\times(\text{HH}\mod12+\dfrac{\text{MM}}{60}),6\times\text{MM}\)。

Code

别试了，不和样例一模一样，但答案保证是对的。

#include <cstdio>
#include <algorithm>
using namespace std;

int h, m;

int main() {
	scanf("%d:%d", &h, &m);
	printf("%.1lf %d\n", ((h % 12) + m / 60.0) * 30, m * 6);
}