「题解」agc031_c Differ by 1 Bit

本文将同步发布于：

题目

题目链接：洛谷 AT4693、AtCoder agc031_c。

题意概述

给定三个数 $n,a,b$，求一个 $0\sim 2^n-1$ 的排列满足下列三个条件：

$p_1=a$；
$p_{2^n}=b$；
$\operatorname{popcount}(p_i\oplus p_{i+1})=1$，其中 $\oplus$ 表示按位异或。

请你判定是否可以构造并输出方案（若可以）。

题解

启发式的画图

直接考虑这个问题，似乎有些困难？

我们先用简单的语言，将它转化为一个图论问题。

图论转化

如果两个整数 $a,b\in[0,2^n)$，满足 $\operatorname{popcount}(a\oplus b)=1$，那么我们就在 $a,b$ 之间连一条边。

那么问题转化为了给定起点与终点，求一条长度为 $2^n$ 的简单路径。

转化成了图论问题，我们肯定要用几何直观来看看这个图到底是什么样子，采用画图工具 Graph Editor，取 $n=2,3$ 时：

图片 $n=2$：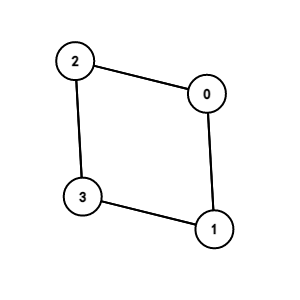

图片 $n=3$：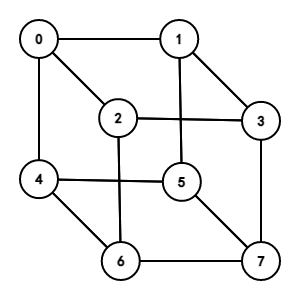

这提醒我们，整个图将会形成一个 $n$ 维立方体。

具体地，我们考虑证明这件事，非常简单，换个角度即可。我们将一个二进制数各位上的数分开，看作各个维度的坐标值，例如 $0=(00)_2\to (0,0),2=(10)_2\to (1,0)$。那么我们不难得到此结论。

熟练解决图论问题

我们不难发现，这个图是一个二分图，其中左部点编号对应的二进制数中 $1$ 的个数为偶数，右部点编号对应的二进制数中 $1$ 的个数为奇数。

我们由此得到结论，如果存在答案，那么 $\operatorname{popcount}(a\oplus b)\equiv 1\pmod 2$。

这个条件对解的必要性已经得到证明，下面我们通过构造来证明其充分性。

构造与递推

首先为了化简问题，我们不难发现从 $a$ 走到 $b$ 等价于从 $0$ 走到 $a\oplus b$，这是因为异或的自反律与交换律，即 $p_i\oplus x\oplus p_{i+1}\oplus x=p_i\oplus p_{i+1}$。

对于 $n$ 维立方体，它一定是由两个 $n-1$ 维立方体上下拼接而成。

因此，我们考虑用类似数学归纳法的方式进行构造。

我们具有归纳基础，因为显然我们会 $n=1$ 时的情况（一条线段从 $0$ 走到 $1$）；

我们考虑如何通过 $n-1$ 维的方案构造 $n$ 维的方案，我们决定分类讨论：

根据上面的理论，我们分类讨论终点的位置（起点为 $0$）；
终点 $t$ 与起点在不同的层：我们找到一条合法的从起点走 $n-1$ 维空间到达 $x$ 的方案，然后 $x$ 走到另一层对应的点 $x'$，再在 $n-1$ 维空间中从 $0$ 走到 $t\oplus x'$ 的方案，$x$ 可任取；
终点 $t$ 与起点在同一层：我们直接从 $0$ 走到 $t$，然后把路径从路径中任意两个相邻点之间直接分割开来，在中间插入一个下层的 $n-1$ 维的路径。

上面的文字叙述可能有点难懂，我们画个三维空间的图：

第一种情况：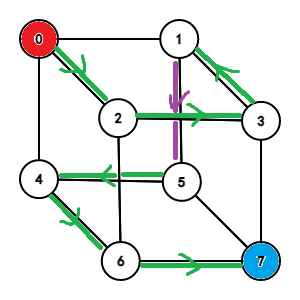

第二种情况：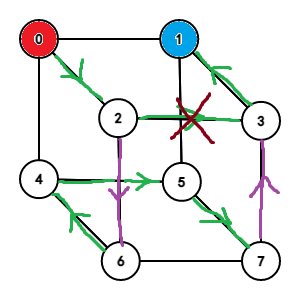

至此，我们用构造的方法证明了条件的充分性，可解决本题。

时间复杂度为 $T(n)=2T(n-1)+\Theta(2^n)$，分析可知为 $\Theta(2^nn)$。

参考程序

参考程序中情况一选取 $x=1$，情况二选取起点和路径的第二个点。

__builtin_parity(x) 表示求 $x$ 的二进制表示中 $1$ 的个数的奇偶性，奇数为 $1$，偶数为 $0$。

#include<bits/stdc++.h>

using namespace std;

#define reg register

typedef long long ll;

#define flush() (fwrite(wbuf,1,wp1,stdout),wp1=0)

#define putchar(c) (wp1==wp2&&(flush(),0),wbuf[wp1++]=c)

static char wbuf[1<<21];int wp1;const int wp2=1<<21;

inline void write(reg int x){

	static char buf[32];

	reg int p=-1;

	if(!x) putchar('0');

	else while(x) buf[++p]=(x%10)^'0',x/=10;

	while(~p) putchar(buf[p--]);

	return;

}

inline void writeln(const char *s){

	while(*s) putchar(*(s++));

	putchar('\n');

	return;

}

const int MAXN=17;

inline void solve(reg int x,reg int a,reg int ans[]){

	if(!x)

		ans[0]=0;

	else if(x==1)

		ans[0]=0,ans[1]=1;

	else{

		reg int val=1<<(x-1);

		if(a&val){

			solve(x-1,1,ans),solve(x-1,a^(val+1),ans+val);

			for(reg int i=val;i<(1<<x);++i)

				ans[i]=ans[i]^(val+1);

		}

		else{

			solve(x-1,a,ans),solve(x-1,ans[1],ans+val);

			for(reg int i=val;i<(1<<x);++i)

				ans[i]=ans[i]^val;

			static int tmp[1<<MAXN];

			tmp[0]=ans[0];

			for(reg int i=0;i<val;++i)

				tmp[i+1]=ans[i+val];

			for(reg int i=val+1;i<(1<<x);++i)

				tmp[i]=ans[i-val];

			for(reg int i=0;i<(1<<x);++i)

				ans[i]=tmp[i];

		}

	}

	return;

}

int n,A,B;

int ans[1<<MAXN];

int main(void){

	scanf("%d%d%d",&n,&A,&B);

	B^=A;

	if(__builtin_parity(B)){

		writeln("YES");

		solve(n,B,ans);

		reg int U=(1<<n)-1;

		for(reg int i=0;i<=U;++i)

			write(ans[i]^A),putchar(i==U?'\n':' ');

	}

	else

		writeln("NO");

	flush();

	return 0;

}