Kernel Methods for Deep Learning

引
主要内容
- 与深度学习的联系
实验

Cho Y, Saul L K. Kernel Methods for Deep Learning[C]. neural information processing systems, 2009: 342-350.

@article{cho2009kernel,

title={Kernel Methods for Deep Learning},

author={Cho, Youngmin and Saul, Lawrence K},

pages={342--350},

year={2009}}

引

这篇文章介绍了一种新的核函数, 其启发来自于神经网络的运算.

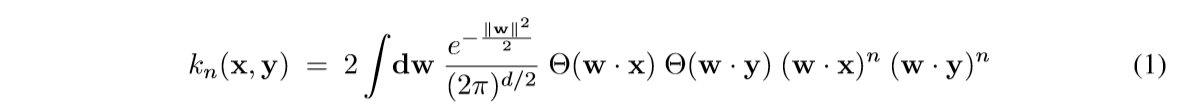
其中$\Theta(z)=\frac{1}{2}(1+\mathrm{sign}(z))$.

主要内容

主要性质, 公式(1)可以表示成:

\[k_n(\mathbf{x}, \mathbf{y}) = \frac{1}{\pi} \|\mathbf{x}\|^n\|\mathbf{y}\|^n J_n(\theta).
\tag{2}
\]

其中:

\[J_n(\theta) = (-1)^n (\sin \theta)^{2n+1} (\frac{1}{\sin \theta} \frac{\partial}{\partial \theta})^n(\frac{\pi-\theta}{\sin \theta}).
\tag{3}
\]

\[\theta = \cos^{-1} (\frac{\mathbf{x}\cdot \mathbf{y}}{\|\mathbf{x}\| \|\mathbf{y}\|}).
\tag{4}
\]

特别的:

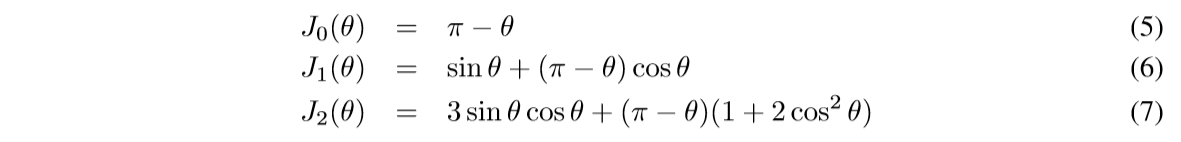
其证明如下:

第(17)的证明我没有推, 因为 contour integration 暂时不了解.

细心的读者可能会发现, 最后的结果是$\frac{\partial^n}{\partial(\cos \theta)^n}$, 注意对于一个函数$f(\cos \theta)$, 我们可以令$g(\theta) = f(\cos \theta)$则:

\[\frac{\partial f}{\partial \cos \theta} = \frac{\partial{g}}{\partial \theta} \frac{\partial\theta}{\partial \cos \theta},
\]

又

\[\mathrm{d}\cos \theta =-\sin \theta \mathrm{d} \theta.
\]

便得结论.

与深度学习的联系

如果我们把注意力集中在某一层, 假设输入为$\mathbf{x}$, 输出为:

\[\mathbf{f}(\mathbf{x}) = g(W\mathbf{x}) \in \mathbb{R}^m,
\]

其中$g(z) = \Theta(z) z^n$是激活函数, 不同的n有如下的表现:

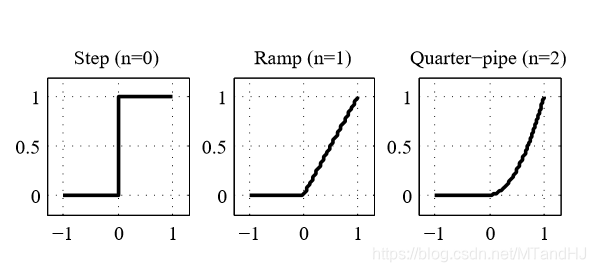
$n=1$便是我们熟悉的ReLU.

考虑俩个输入$\mathbf{x},\mathbf{y}$所对应的输出$\mathbf{f}(\mathbf{x}),\mathbf{f}(\mathbf{y})$的内积:

\[\mathbf{f}(\mathbf{x}) \cdot \mathbf{f}(\mathbf{y}) = \sum_{i=1}^m \Theta(\mathbf{w}_i \cdot \mathbf{x}) \Theta(\mathbf{w}_i \cdot \mathbf{y}) (\mathbf{w}_i \cdot \mathbf{x})^n (\mathbf{w}_i \cdot \mathbf{y})^n
\]

如果每个权重$W_{ij}$都服从标准正态分布, 则:

\[\lim_{m \rightarrow \infty} \frac{2}{m} \mathbf{f} (\mathbf{x}) \cdot \mathbf{f}(\mathbf{x}) = k_n(\mathbf{x}, \mathbf{y}).
\]

实验

实验失败了, 代码如下.

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

from sklearn.svm import NuSVC

"""

Arc_cosine kernel

"""

class Arc_cosine:

    def __init__(self, n=1):

        self.n = n

        self.own_kernel = self.kernels(n)

    def kernel0(self, x, y):

        norm_x = np.linalg.norm(x)

        norm_y = np.linalg.norm(y)

        cos_value = x @ y / (norm_x *

                             norm_y)

        angle = np.arccos(cos_value)

        return 1 - angle / np.pi

    def kernel1(self, x, y):

        norm_x = np.linalg.norm(x)

        norm_y = np.linalg.norm(y)

        cos_value = x @ y / (norm_x *

                    norm_y)

        angle = np.arccos(cos_value)

        sin_value = np.sin(angle)

        return (norm_x * norm_y) ** self.n * \

               (sin_value + (np.pi - angle) *

                cos_value) / np.pi

    def kernel2(self, x, y):

        norm_x = np.linalg.norm(x)

        norm_y = np.linalg.norm(y)

        cos_value = x @ y / (norm_x *

                             norm_y)

        angle = np.arccos(cos_value)

        sin_value = np.sin(angle)

        return (norm_x * norm_y) ** self.n * \

               3 * sin_value * cos_value + \

               (np.pi - angle) * (1 + 2 * cos_value ** 2)

    def kernels(self, n):

        if n is 0:

            return self.kernel0

        elif n is 1:

            return self.kernel1

        elif n is 2:

            return self.kernel2

        else:

            raise ValueError("No such kernel, n should be "

                             "0, 1 or 2")

    def kernel(self, X, Y):

        m = X.shape[0]

        n = Y.shape[0]

        C = np.zeros((m, n))

        for i in range(m):

            for j in range(n):

                C[i, j] = self.own_kernel(

                    X[i], Y[j]

                )

        return C

    def __call__(self, X, Y):

        return self.kernel(X, Y)

在俩个数据上进行SVM, 数据如下:

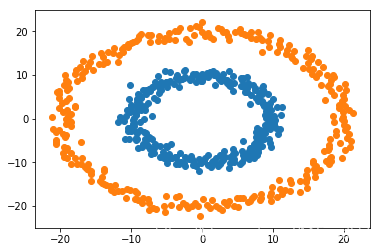
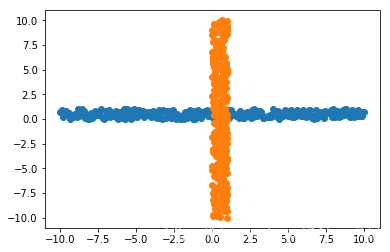
在SVM上跑:

'''

#生成圈圈数据

def generate_data(circle, r1, r2, nums=300):

    variance = 1

    rs1 = np.random.randn(nums) * variance + r1

    rs2 = np.random.randn(nums) * variance + r2

    angles = np.linspace(0, 2*np.pi, nums)

    data1 = (rs1 * np.sin(angles) + circle[0],

            rs1 * np.cos(angles) + circle[1])

    data2 = (rs2 * np.sin(angles) + circle[0],

            rs2 * np.cos(angles) + circle[1])

    df1 = pd.DataFrame({'x':data1[0], 'y': data1[1],

                        'label':np.ones(nums)})

    df2 = pd.DataFrame({'x':data2[0], 'y': data2[1],

                        'label':-np.ones(nums)})

    return df1, df2

'''

#生成十字数据

def generate_data(left, right, down, up,

                  circle=(0., 0.), nums=300):

    variance = 1

    y1 = np.random.rand(nums) * variance + circle[1]

    x2 = np.random.rand(nums) * variance + circle[0]

    x1 = np.linspace(left, right, nums)

    y2 = np.linspace(down, up, nums)

    df1 = pd.DataFrame(

        {'x': x1,

         'y': y1,

         'label':np.ones_like(x1)}

    )

    df2 = pd.DataFrame(

        {'x': x2,

         'y': y2,

         'label':-np.ones_like(x2)}

    )

    return df1, df2

def pre_test(left, right, func, nums=100):

    x1, y1 = left

    x2, y2 = right

    x = np.linspace(x1, x2, nums)

    y = np.linspace(y1, y2, nums)

    X,Y = np.meshgrid(x,y)

    m, n = X.shape

    Z = func(np.vstack((X.reshape(1, -1),

             Y.reshape(1, -1))).T).reshape(m, n)

    return X, Y, Z

df1, df2 = generate_data(-10, 10, -10, 10)

df = df1.append(df2)

classifer2 = NuSVC(kernel=Arc_cosine(n=1))

classifer2.fit(df.iloc[:, :2], df['label'])

X, Y, Z = pre_test((-10, -10), (10, 10), classifer2.predict)

plt.contourf(X, Y, Z)

plt.show()

预测结果均为:

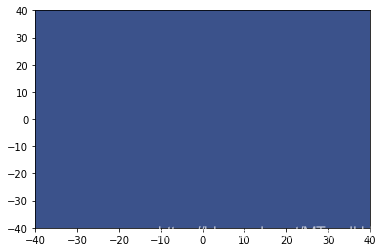
而在一般的RBF上, 结果都是很好的:

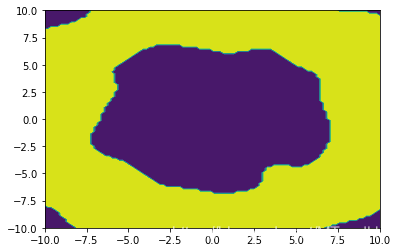
在多项式核上也ok:

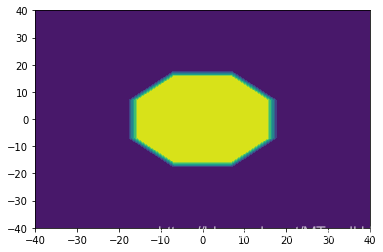
如果有人能发现代码中的错误，请务必指正.