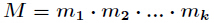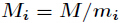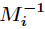BGV方案
BGV方案


SIMD技术



中国剩余定理
在《孙子算经》中有这样一个问题:“今有物不知其数,三三数之剩二(除以3余2),五五数之剩三(除以5余3),七七数之剩二(除以7余2),问物几何?”这个问题称为“孙子问题”,该问题的一般解法国际上称为“中国剩余定理”。
简单点说就是求x,使其满足: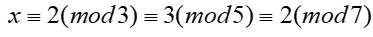
我们的主要求解方法分为三步:
- 找出三个数:从3和5的公倍数中找出被7除余1的最小数15,从3和7的公倍数中找出被5除余1 的最小数21,最后从5和7的公倍数中找出除3余1的最小数70。
- 用15乘以2(2为最终结果除以7的余数),用21乘以3(3为最终结果除以5的余数),同理,用70乘以2(2为最终结果除以3的余数),然后把三个乘积相加(15*2+21*3+70*2)得到和233。
- 用233除以3,5,7三个数的最小公倍数105,得到余数23,即233%105=23。这个余数23就是符合条件的最小数。
算法分析
我们将“孙子问题”拆分成几个简单的小问题,从零开始,试图揣测古人是如何推导出这个解法的。
首先,我们假设n1是满足除以3余2的一个数,比如2,5,8等等,也就是满足3*k+2(k>=0)的一个任意数。同样,我们假设n2是满足除以5余3的一个数,n3是满足除以7余2的一个数。
有了前面的假设,我们先从n1这个角度出发,已知n1满足除以3余2,能不能使得 n1+n2 的和仍然满足除以3余2?进而使得n1+n2+n3的和仍然满足除以3余2?
这就牵涉到一个最基本数学定理,如果有a%b=c,则有(a+kb)%b=c(k为非零整数),换句话说,如果一个除法运算的余数为c,那么被除数与k倍的除数相加(或相减)的和(差)再与除数相除,余数不变。这个是很好证明的。
以此定理为依据,如果n2是3的倍数,n1+n2就依然满足除以3余2。同理,如果n3也是3的倍数,那么n1+n2+n3的和就满足除以3余2。这是从n1的角度考虑的,再从n2,n3的角度出发,我们可推导出以下三点:
- 为使n1+n2+n3的和满足除以3余2,n2和n3必须是3的倍数。
- 为使n1+n2+n3的和满足除以5余3,n1和n3必须是5的倍数。
- 为使n1+n2+n3的和满足除以7余2,n1和n2必须是7的倍数。
因此,为使n1+n2+n3的和作为“孙子问题”的一个最终解,需满足:
- n1除以3余2,且是5和7的公倍数。
- n2除以5余3,且是3和7的公倍数。
- n3除以7余2,且是3和5的公倍数。
所以,孙子问题解法的本质是从5和7的公倍数中找一个除以3余2的数n1,从3和7的公倍数中找一个除以5余3的数n2,从3和5的公倍数中找一个除以7余2的数n3,再将三个数相加得到解。在求n1,n2,n3时又用了一个小技巧,以n1为例,并非从5和7的公倍数中直接找一个除以3余2的数,而是先找一个除以3余1的数,再乘以2。
这里又有一个数学公式,如果a%b=c,那么(a*k)%b=a%b+a%b+…+a%b=c+c+…+c=kc(k>0),也就是说,如果一个除法的余数为c,那么被除数的k倍与除数相除的余数为kc。展开式中已证明。
最后,我们还要清楚一点,n1+n2+n3只是问题的一个解,并不是最小的解。如何得到最小解?我们只需要从中最大限度的减掉3,5,7的公倍数105即可。道理就是前面讲过的定理“如果a%b=c,则有(a-kb)%b=c”。所以(n1+n2+n3)%105就是最终的最小解。
总结
经过分析发现,中国剩余定理的孙子解法就是以下两个基本数学定理的灵活运用:
- 如果 a%b=c , 则有 (a+kb)%b=c (k为非零整数)。
- 如果 a%b=c,那么 (a*k)%b=kc (k为大于零的整数)。
扩展算法
设正整数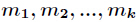 两两互素,则同余方程组
两两互素,则同余方程组
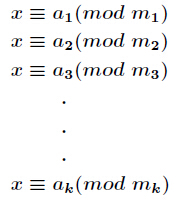
有整数解。并且在模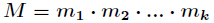 下的解是唯一的,解为
下的解是唯一的,解为
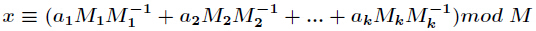

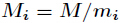 ,而
,而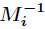 为
为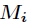 模
模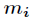 的逆元。
的逆元。
代码:
int CRT(int a[],int m[],int n)
{
int M = 1;
int ans = 0;
for(int i=1; i<=n; i++)
M *= m[i];
for(int i=1; i<=n; i++)
{
int x, y;
int Mi = M / m[i];
extend_Euclid(Mi, m[i], x, y);
ans = (ans + Mi * x * a[i]) % M;
}
if(ans < 0) ans += M;
return ans;
}
多项式中国剩余定理



求乘法逆元
有两种方法:
1、费马小定理
该方法速度非常快

求逆元代码:
#include <stdio.h>
#include <math.h> int main()
{
int m, n, x;
puts(" 基于费马定理求逆元\n");
puts(" 对m * x = 1 mod n,求x\n");
printf("请输入m=");
scanf("%d", &m);
printf("请输入n=");
scanf("%d", &n);
x = (int)pow(m, n - 2) % n;
printf("x=%d\n", x);
system("pause");
return 0;
}
2、扩展欧几里得

扩展欧几里得算法实现:
#include<iostream>
using namespace std; //递归求解
int exgcd(int a, int b, int& x, int& y)
{
if (b == 0)
{
x = 1;
y = 0;
return a;
}
int gcd = exgcd(b, a % b, x, y);
int x2 = x, y2 = y;
x = y2;
y = x2 - (a / b) * y2;
return gcd;
} //非递归求解
int exgcd01(int a, int b, int& x, int& y)
{
int x1, y1, x0, y0;
x0 = 1; y0 = 0;
x1 = 0; y1 = 1;
x = 0; y = 1;
int r = a % b;
int q = (a - r) / b;
while (r)
{
x = x0 - q * x1; y = y0 - q * y1;
x0 = x1; y0 = y1;
x1 = x; y1 = y;
a = b; b = r; r = a % b;
q = (a - r) / b;
}
return b;
} int main()
{
int x, y, a, b,option;
cout << "扩展欧几里得算法" << endl;
cout << endl << "请选择:1、递归求解;2、非递归求解" << endl;
cin >> option;
if (option == 1)
{
cout << "请输入a和b:" << endl;
cin >> a >> b;
cout << "a和b的最大公约数:" << endl;
cout << exgcd(a, b, x, y) << endl;
cout << "ax+by=gcd(a,b) 的一组解是:" << endl;
cout << x << " " << y << endl;
}
else if (option == 2)
{
cout << "请输入a和b:" << endl;
cin >> a >> b;
cout << "a和b的最大公约数:" << endl;
cout << exgcd01(a, b, x, y) << endl;
cout << "ax+by=gcd(a,b) 的一组解是:" << endl;
cout << x << " " << y << endl;
}
else
cout << "请重新输入!" << endl;
return 0;
}
求逆元算法实现:请参考 求逆元
参考
1、云外包密文查询和计算研究-全韩彧
3、扩展欧几里得算法
6、多项式的 “中国剩余定理”-包志超
BGV方案的更多相关文章
- Homomorphic Evaluation of the AES Circuit:解读
之前看过一次,根本看不懂,现在隔这么久,再次阅读,希望有所收获! 论文版本:Homomorphic Evaluation of the AES Circuit(Updated Implementati ...
- 分布式锁1 Java常用技术方案
前言: 由于在平时的工作中,线上服务器是分布式多台部署的,经常会面临解决分布式场景下数据一致性的问题,那么就要利用分布式锁来解决这些问题.所以自己结合实际工作中的一些经验和网上看到的一些资 ...
- 再谈C#采集,一个绕过高强度安全验证的采集方案?方案很Low,慎入
说起采集,其实我是个外行,以前拔过阿里巴巴的客户数据,在我博客的文章:C#+HtmlAgilityPack+XPath带你采集数据(以采集天气数据为例子) 中,介绍过采集用的工具,其实很Low的,分析 ...
- 谈谈一些有趣的CSS题目(八)-- 纯CSS的导航栏Tab切换方案
开本系列,谈谈一些有趣的 CSS 题目,题目类型天马行空,想到什么说什么,不仅为了拓宽一下解决问题的思路,更涉及一些容易忽视的 CSS 细节. 解题不考虑兼容性,题目天马行空,想到什么说什么,如果解题 ...
- iOS开发之多种Cell高度自适应实现方案的UI流畅度分析
本篇博客的主题是关于UI操作流畅度优化的一篇博客,我们以TableView中填充多个根据内容自适应高度的Cell来作为本篇博客的使用场景.当然Cell高度的自适应网上的解决方案是铺天盖地呢,今天我们的 ...
- 尝试asp.net mvc 基于controller action 方式权限控制方案可行性
微软在推出mvc框架不久,短短几年里,版本更新之快,真是大快人心,微软在这种优秀的框架上做了大量的精力投入,是值得赞同的,毕竟程序员驾驭在这种框架上,能够强力的精化代码,代码层次也更加优雅,扩展较为方 ...
- Redis百亿级Key存储方案(转)
1 需求背景 该应用场景为DMP缓存存储需求,DMP需要管理非常多的第三方id数据,其中包括各媒体cookie与自身cookie(以下统称supperid)的mapping关系,还包括了supperi ...
- Android 几种消息推送方案总结
转载请注明出处:http://www.cnblogs.com/Joanna-Yan/p/6241354.html 首先看一张国内Top500 Android应用中它们用到的第三方推送以及所占数量: 现 ...
- WebGIS中等值面展示的相关方案简析
文章版权由作者李晓晖和博客园共有,若转载请于明显处标明出处:http://www.cnblogs.com/naaoveGIS/ 1.背景 等值面是气象.环保等相关项目上常用到的效果展示.在传统的CS项 ...
随机推荐
- 攻防世界(九)PHP2
攻防世界系列:PHP2 1.打开什么信息也没有. 尝试各种首页index.php index.html 加 [F12]没有结果,最后发现是index.phps .phps文件是什么? phps文件就 ...
- IT菜鸟之OSI七层模型
OSI七层模型从下到上分别是: 应用层 表示层 会话层 传输层 网络层 数据链路层 物理层 第一层物理层: 物理层是传输媒介(网线.无线.光纤) 在线路中起到的作用:是将0/1转换成电信号或光信号 物 ...
- mysql数据库-日志管理
MySQL 支持丰富的日志类型 事务日志:transaction log 事务日志的写入类型为"追加",因此其操作为"顺序IO":通常也被称为:预写式日志 wr ...
- ShardingSphere你还不会吗?(第一篇)
ShardingSphere你还不会吗?(第一篇) 作者:星晴(当地小有名气,小到只有自己知道的杰伦粉) 一.需求 我们做项目的时候,数据量比较大,单表千万级别的,需要分库分表,于是在网上搜索这方面的 ...
- 【排除解决】System.Runtime.InteropServices.ExternalException (0x80004005): GDI+ 中发生一般性错误
前言: 今天项目发布上线,发布到正式环境验证功能的时候忽然方向之前做的一个图片合成的功能报错了提示:System.Runtime.InteropServices.ExternalException ( ...
- Go语言实现Snowflake雪花算法
转载请声明出处哦~,本篇文章发布于luozhiyun的博客:https://www.luozhiyun.com/archives/527 每次放长假的在家里的时候,总想找点简单的例子来看看实现原理,这 ...
- CVPR2020最新论文扫描盘点(上)
CVPR2020最新论文扫描盘点(上) 最近计算机视觉三大顶会之一CVPR2020接收结果已经公布,一共有1470篇论文被接收,接收率为22%,相比去年降低3个百分点,竞争越来越激烈.这里整理来自Tw ...
- 北汽极狐ARCFOX与华为合作
北汽极狐ARCFOX与华为合作 全球首款激光雷达量产车 2021年,是激光雷达"上车"的元年. 曾经价格高不可攀,只能用于Robotaxi.无人车测试的激光雷达,终于彻底具备商业化 ...
- HDR sensor 原理介绍
HDR sensor 原理介绍 一. HDR sensor 原理介绍 1. 什么是sensor的动态范围(dynamic range): sensor的动态范围就是sensor在一幅图像里能够同时体现 ...
- Contos8 安装 MariaDb 时报错:Could not open mysql.plugin table: table mysql.plugin
导语: 因个人服务器误删了一些文件导致MariaDB崩溃,一直在报错,所以想着重装一下,没想到在重装后启动时再次报错(与之前报错不同),这次的报错原因大致是因为某些插件表找不到. 因此又开启了漫长的寻 ...