KMP（The Knuth-Morris-Pratt Algorithm）

本文代码来自于中国大学MOOC

KMP课件下载

注释内容为自己理解，如有错误请评论，或者私信给我，谢谢

#include <stdio.h>
#include "stdlib.h"
#include "string.h"

typedef int Position;

Position KMP(char string[25], char pattern[7]);

void BuildMatch(char *pattern, int *pInt);

#define NotFound -1

int main() {
    char string[] = "this is a simple example";
    char pattern[] = "simple";
    Position p = KMP(string, pattern);
    if (p == NotFound) printf("Not found.\n");
    else {
        printf("%s\n", string + p);
        printf("%f\n", p);
    }
    return 0;
}

Position KMP(char *string, char *pattern) {
    int n = strlen(string);
    int m = strlen(pattern);
    int s, p, *match;

    if (m > n) return NotFound;
    match = (int *) malloc(sizeof(int) * m);
    // 查询match最长匹配字符串位置值 例如：图1-1
    // pattern a    b   c   a   b
    // index   0    1   2   3   4
    // match   -1   -1  -1  0   1
    BuildMatch(pattern, match);

    s = p = 0;
    while (s < n && p < m) {
        if (string[s] == pattern[p]) {
            s++;
            p++;
        } else if (p > 0) {
            // 将p置为 前p-1个元素 最大子串长度+1
            // 如图1-2
            p = match[p - 1] + 1;
        } else
            s++;
    }
    return (p == m) ? (s - m) : NotFound;
}

void BuildMatch(char *pattern, int *match) {
    int i, j;
    int m = strlen(pattern);
    match[0] = -1;// -1 表示子串长度不存在，无任何相同的元素
    for (int j = 1; j < m; ++j) {
        // i表示前j-1个元素最大相同子串长度 数组索引位置 index-length 0-1
        i = match[j - 1];

        while ((i >= 0) && (pattern[i + 1] != pattern[j]))
            // 第j个下标的字符和(match[j-1]+1)下标上的元素比较
            // 如果不匹配，则根据下标为match[j-1]的相同串基础上进行条件比较
            // 因为match[j-1]已经存在，那么绿紫色整块和后面绿紫块肯定一样
            // 又第一个小绿块为match[match[j-1]]，绿块和紫块相同
            // 所以第一个绿块和最后一个紫块相同，只需比较问号位置的值即可
            // char[match[match[j-1]]+1] 和 char[j] 的值是否相等
            // 如图 1-3
            i = match[i];

        if (pattern[i + 1] == pattern[j])
            // 如图 1-4
            match[j] = i + 1;
            // 如果都匹配不上就直接设置为-1
        else match[j] = -1;
    }
}

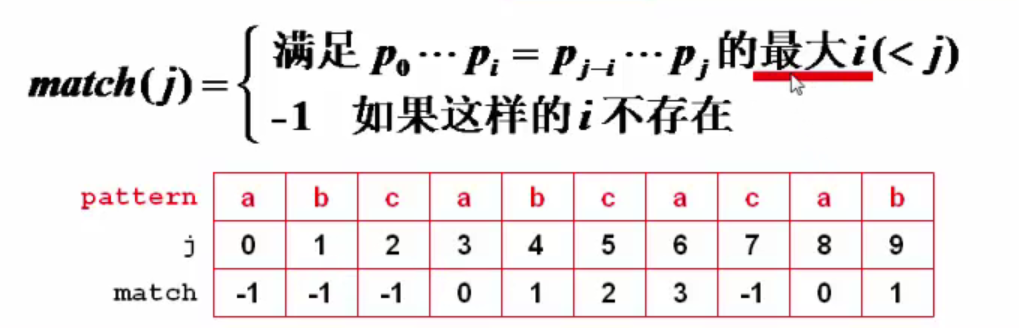
match[j]的值实际上是前j个（包括j）元素的最大子串长度 对应到数组中的位置 比如图中 j = 6; 最大子串(abca)的长度为4,

在数组中的索引为3

当比较到后面不相等时，模式串相当于要后移到从上往下的第三个横条的情形，也就是把第二个横条情况p = match[p-1]+1

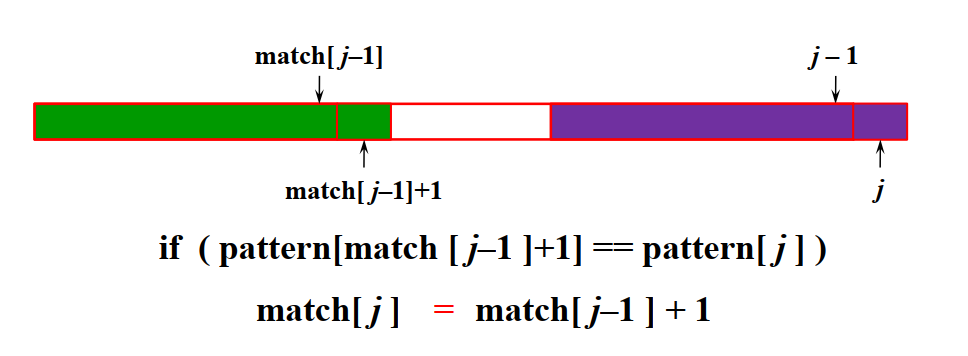
• 第j个下标的字符和(match[j-1]+1)下标上的元素比较
• 如果不匹配，则根据下标为match[j-1]的相同串基础上进行条件比较
• 因为match[j-1]已经存在，那么绿紫色整块和后面绿紫块肯定一样
• 又第一个小绿块为match[match[j-1]]，绿块和紫块相同
• 所以第一个绿块和最后一个紫块相同，只需比较问号位置的值即可
• char[match[match[j-1]]+1] 和 char[j] 的值是否相等

---