字符串与模式匹配算法（六）：Needleman–Wunsch算法

一、Needleman-Wunsch 算法

　　尼德曼-翁施算法（英语：Needleman-Wunsch Algorithm）是基于生物信息学的知识来匹配蛋白序列或者DNA序列的算法。这是将动态算法应用于生物序列的比较的最早期的几个实例之一。该算法是由 Saul B. Needlman和 Christian D. Wunsch 两位科学家于1970年发明的。本算法高效地解决了如何将一个庞大的数学问题分解为一系列小问题，并且从一系列小问题的解决方法重建大问题的解决方法的过程。该算法也被称为优化匹配算法和整体序列比较法。时至今日尼德曼-翁施算法仍然被广泛应用于优化整体序列比较中。

二、初始化得分矩阵

　　首先建立如下的得分矩阵。从第一列第一行的位置起始。计算过程从d _0,0开始，可以是按行计算，每行从左到右，也可以是按列计算，每列从上到下。当然，任何计算过程，只要满足在计算 d_{(i , j)} 时 d _{(i-1, j)}（上边）、d _{(i-1 , j-1)} （左上）和 d_{(i, j-1)} （左边）都已经被计算这个条件即可。在计算 d_{(i , j)}后，需要保存d_{(i , j)}是从 d _{(i-1 , j)} 、d_{(i-1 , j-1)} 或 d_{(i, j-1)} 中的一个推进的，或保存计算的路径，以便于后续处理。上述计算过程到 d_{(m , n)} 结束，其中m，n各位两个序列的长度。

		G	C	A	T	G	C	U
	0
G
A
T
T
A
C
A

三、选择得分体系

　　我们可以看出每个位置配对都有三种可能情况：匹配， 不匹配与错位（或插入）：

• 匹配： 两个字母相同

• 不匹配：两个字母不相同

• 错位：一个字母与另一个序列中的间隔（空白）相匹配

　　这三种得分情况有很多打分标准，这些情况都总结在得分体系的部分。从现在开始，我们将使用Needleman 和Wunsch创造的简单体系来进行打分，即匹配得1分，不匹配得-1分，错位得-1分.

四、填充评分矩阵

　　开始于第二行中的第二列，初始值为0。通过矩阵一行一行移动，计算每个位置的分数。得分被计算为从现有的分数可能的最佳得分（即最高）的左侧，顶部或左上方（对角线）。当一个得分从顶部计算，或从左边这代表在我们的对准的插入缺失。当我们从对角线计算分数这表示两个字母所得位置匹配的对准。定不存在“向上”或“左上”的位置对第二行，我们只能从现有单元向左添加。因此，我们添加-1的权利，因为这代表了从以前的比分插入缺失。这导致在第一行是0，-1，-2，-3，-4，-5，-6，-7。这同样适用于第二列，因为我们只具有以上现有分数。因此，我们有：

		G	C	A	T	G	C	U
	0	-1	-2	-3	-4	-5	-6	-7
G	-1
A	-2
T	-3
T	-4
A	-5
C	-6
A	-7

　　第一种情况是存在向三个方向构筑矩阵，周围位置得分如下：

		G
	0	-1
G	-1	?

　　该单元格具有三个可能的候选总和：

• 对角线的左上邻居的分数为0。G和G的配对是匹配项，因此添加匹配项的分数：0 + 1 = 1
• 正上邻居的得分为-1，从那里移动代表一个indel，因此将indel的得分相加：（-1）+（-1）=（-2）
• 左邻居的得分也为-1，代表插入缺失，也产生（-2）。

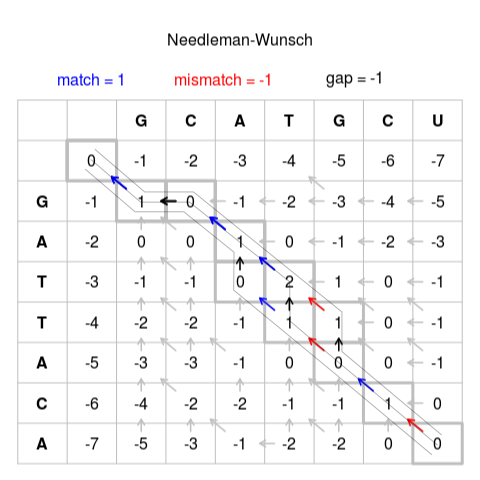
　　得分最高的单元格也必须记录下来。在的文章最开始说的那矩阵图中，它表示为从行和列3中的单元格到行和列2中的单元格的箭头，?号处根据评分规则最后为1。

　　对接下来的位置，我们有不同的选择。

		G	C
	0	-1	-2
G	-1	1	X
A	-2	Y

　　X:

• 上: (-2)+(-1) = (-3)

• 左: (+1)+(-1) = (0)

• 左上: (-1)+(-1) = (-2)

　　Y:

• 上: (1)+(-1) = (0)

• 左: (-2)+(-1) = (-3)

• 左上: (-1)+(-1) = (-2)

　　对于X和Y，最高得分均为0。
　　两个或所有相邻小格可能会达到最高的候选分数：

	T	G
T	1	1
A	0	X

• Top: (1)+(-1) = (0)

• Top-Left: (1)+(-1) = (0)

• Left: (0)+(-1) = (-1)

　　在这种情况下，必须将达到最高候选得分的所有方向记录为中并完成图中可能的起点，例如，在第7行和第7列的单元格中。

　　以这种方式填写表格会给出分数或所有可能的比对候选，右下角单元格中的分数代表最佳比对的比对分数。

五、追溯本源

　　按照箭头的方向标记从右下角的单元格到左上角的单元格的路径。从此路径开始，将按照以下规则构建序列：

• 对角箭头表示匹配或不匹配，因此原始单元格的列字母和行字母将对齐。

• 水平或垂直箭头表示插入/缺失。 水平箭头将使间隙（“-”）与行的字母（“侧边”序列）对齐，垂直箭头将使间隙与列的字母（“顶部”序列）对齐。

• 如果有多个箭头可供选择，则它们表示路线的分支。 如果两个或多个分支都属于从右下角到左上角单元格的路径，则它们是同等可行的路线。 在这种情况下，请注意将路径作为单独的对齐候选。

　　遵循这些规则，上图中的一个可能的对齐候选者的步骤为：

U → CU → GCU → -GCU → T-GCU → AT-GCU → CAT-GCU → GCAT-GCU
A → CA → ACA → TACA → TTACA → ATTACA → -ATTACA → G-ATTACA
             ↓
    (branch) → TGCU → ...
             → TACA → ...

六、评分系统

　　最简单的计分方案只是为每个匹配，不匹配和插入缺失给出一个值。 上面的分步指南使用match = 1，mismatch = -1，indel = -1。 因此，对准分数越低，编辑距离越大，因为该计分系统需要较高的分数。 另一个计分系统可能是：

• Match = 0

• Indel = 1

• Mismatch = 1

　　对于此系统，对齐分数将代表两个字符串之间的编辑距离。 可以针对不同的情况设计不同的评分系统，例如，如果认为差距对您的对齐方式非常不利，则可以使用对差距进行严重惩罚的评分系统，例如：

• Match = 0

• Mismatch = 1

• Indel = 10

七、Needleman–Wunsch算法代码

　　计算评分矩阵，按行推进，根据左、上、左上计算的结果取最大的：

 1     /**
 2      * 一种用于计算全局最大相似度矩阵的实用方法。
 3      *
 4      * @param sequence1 代表第一个氨基酸序列的字符串。
 5      * @param sequence1 代表第二个氨基酸序列的字符串。
 6      * @param matchScore 代表分配给比赛的分数的浮点数。
 7      * @param mismatchScore 一个浮点数，代表分配给不匹配项的分数。
 8      * @param indelScore 浮点数表示分配给插入和删除的分数。
 9      */
10     public static float[][] computeMatrix(String sequence1, String sequence2, float matchScore, float mismatchScore, float indelScore) {
11         sequence1 = "-" + sequence1;
12         sequence2 = "-" + sequence2;
13
14         float[][] resultMatrix = new float[sequence1.length()][sequence2.length()];
15
16         for (int i = 0; i < sequence1.length(); i++) {
17             resultMatrix[i][0] = i * indelScore;
18         }
19         for (int j = 0; j < sequence2.length(); j++) {
20             resultMatrix[0][j] = resultMatrix[0][j] = j * indelScore;
21         }
22
23         for (int i = 1; i < sequence1.length(); i++) {
24             for (int j = 1; j < sequence2.length(); j++) {
25                 resultMatrix[i][j] = Math.max(resultMatrix[i - 1][j] + indelScore,
26                         Math.max(resultMatrix[i][j - 1] + indelScore, resultMatrix[i - 1][j - 1] +
27                                 (sequence1.charAt(i) == sequence2.charAt(j) ? matchScore : mismatchScore)));
28             }
29         }
30
31         return resultMatrix;
32     }

　　根据评分矩阵来按最低顺序获得最佳对齐：

 1     /**
 2      * 一种计算两个的最佳全局最低对齐序列的实用方法
 3      *
 4      * @param similarityMatrix 2维数组表示以前计算的全局最大相似度矩阵。
 5      * @param sequence1 代表第一个氨基酸序列的字符串。
 6      * @param sequence1 代表第二个氨基酸序列的字符串。
 7      * @param matchScore 代表分配给匹配的分数的浮点数。
 8      * @param mismatchScore 一个浮点数，代表分配给不匹配项的分数。
 9      * @param indelScore 浮点数表示分配给插入和删除的分数。
10      */
11     public static OptimalAlignment obtainOptimalAlignmentByDownmostOrder(float similarityMatrix[][],
12                                                                          String sequence1, String sequence2, double matchScore, double mismatchScore, double indelScore) {
13
14         int i = similarityMatrix.length - 1;
15         int j = similarityMatrix[0].length - 1;
16         StringBuilder alignment1Builder = new StringBuilder();
17         StringBuilder alignment2Builder = new StringBuilder();
18
19         sequence1 = "-" + sequence1;
20         sequence2 = "-" + sequence2;
21
22         while (i != 0 && j != 0) {
23             if (similarityMatrix[i][j] == (similarityMatrix[i][j - 1] + indelScore)) {
24                 alignment1Builder.insert(0, "-");
25                 alignment2Builder.insert(0, sequence2.charAt(j));
26                 j--;
27             } else if (similarityMatrix[i][j] == (similarityMatrix[i - 1][j - 1] + (sequence1.charAt(i) == sequence2.charAt(j) ? matchScore : mismatchScore))) {
28                 alignment1Builder.insert(0, sequence1.charAt(i));
29                 alignment2Builder.insert(0, sequence2.charAt(j));
30                 i--;
31                 j--;
32             } else if (similarityMatrix[i][j] == (similarityMatrix[i - 1][j] + indelScore)){
33                 alignment1Builder.insert(0, sequence1.charAt(i));
34                 alignment2Builder.insert(0, "-");
35                 i--;
36             }
37         }
38
39         return new OptimalAlignment(alignment1Builder.toString(), alignment2Builder.toString());
40     }

　　测试主函数：

 1 　　public static void main(String[] args) {
 2         String sequence1 = "GCATGCU";
 3         String sequence2 = "GATTACA";
 4
 5         float matchScore = 1;
 6         float mismatchScore = -1;
 7         float indelScore = -1;
 8
 9         float[][] computedMatrix = NeedlemanWunsch.computeMatrix(sequence1, sequence2, matchScore, mismatchScore, indelScore);
10
11         System.out.println("Best global downmost alignment: ");
12         System.out.println(NeedlemanWunsch.obtainOptimalAlignmentByDownmostOrder(computedMatrix, sequence1, sequence2, matchScore, mismatchScore, indelScore));
13     }

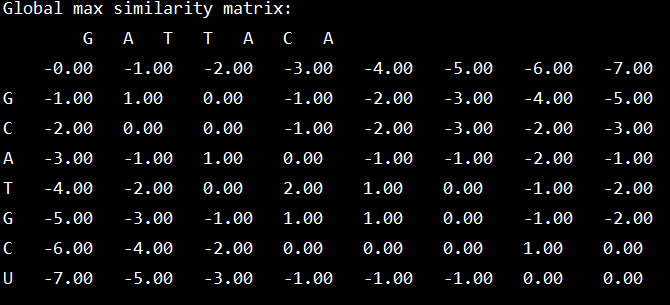
　　全局相似度矩阵：

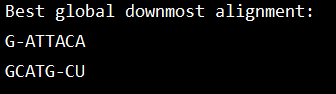
　　结果：