jzoj1497. 景点中心

Description

话说宁波市的中小学生在镇海中学参加计算机程序设计比赛，比赛之余，他们在镇海中学的各个景点参观。镇海中学共有n个景点，每个景点均有若干学生正在参观。这n个景点以自然数1至n编号，每两个景点的编号均不同。每两个景点之间有且只有一条路径。选择哪个景点集中的学生，才能使所有学生走过的路径之和最小呢？

如果存在多个解，则输出距离1最近的那个点，可以证明答案唯一

Input

输入文件center.in中有若干行：

第一行只有一个正整数n，表示景点数。

第二行有n个1至1000间的整数，这n个整数间互相以一个空格分隔。其中第i个整数表示第i个景点处的学生数。

第三行至第n+1行，每行有三个整数I,j,k，表示景点i和景点j之间有一条长尾k的路径直接连接。其中i<>j,1≤i≤n,1≤j≤n;1≤k≤1000。

Output

输出文件center.out中有二行；

第一行只有一个整数i，表示在第i个景点处集中时，所有学生走过的路径之和最短。

第二行也只有一个整数，表示所有学生走过的路径之和的最小值。

Data Constraint

所有的数据均随机生成，且满足：

30%的数据，1≤n≤200。

60%的数据，1≤n≤3000。

100%的数据，1≤n≤100000。

Solution

这题我没想到什么好的方法，主要是靠树形DP推出每个点为集中点时的代价。

首先，我们需要一个初始值，所以我们先暴力将1为集合点时的代价给求出来。

然后我们处理它的子节点





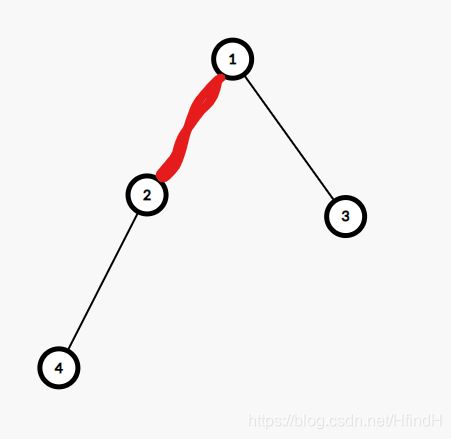
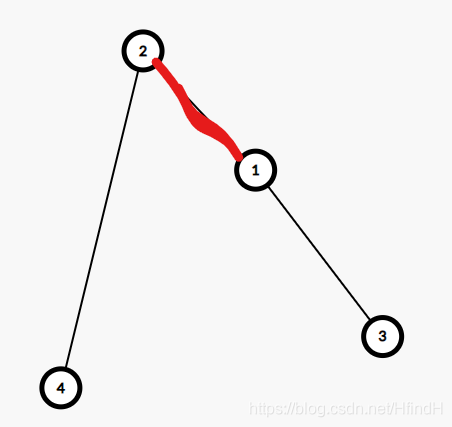
不难发现，子节点与原根节点的连边是条很重要的边

以该子节点为根的子树的每一个节点到集中点的贡献都减少了该边长度，而其他的边都增加了该边长度

所以我们就可以先在第一次暴力求答案的时候先求出几个重要的数

首先我们设tree[i]表示以i为根的子树的学生数

设f[i]表示该点到集中点的贡献

一开始我们求出了f[1]，而其他的点都可以推出来，最后求个最小值即可

Code

#include <cstdio>
#define ll long long
using namespace std;
int len,n,a,b,c,i,ans,go[1000001],to[1000001],last[1000001],w[1000001],tree[1000001],m[1000001];
ll f[1000001];
void make(int x,int y,int z)
{
    go[++len]=y;to[len]=last[x];w[len]=z;last[x]=len;
}
void dg(int x,int fa,ll s1)
{
    int k=last[x];
    tree[x]=m[x];
    f[x]=m[x]*s1;
    while (k)
    {
        if (go[k]!=fa)
		{
			dg(go[k],x,s1+w[k]);
        	tree[x]+=tree[go[k]];
        	f[x]+=f[go[k]];
		}
        k=to[k];
    }
}
void dfs(int x,int fa,ll s)
{
    if (x!=1)
    {
        f[x]=f[fa]+(tree[1]-tree[x])*s-tree[x]*s;
        if (f[x]<f[ans]) ans=x;
    }
    int k=last[x];
    while (k)
    {
        if (go[k]!=fa) dfs(go[k],x,w[k]);
        k=to[k];
    }
}
int main()
{
    scanf("%d",&n);
    for (i=1;i<=n;i++)
    {
        scanf("%d",&m[i]);
    }
    for (i=1;i<n;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        make(a,b,c);make(b,a,c);
    }
    dg(1,0,0);
    ans=1;
    dfs(1,0,0);
    printf("%d\n%lld",ans,f[ans]);
}