X86汇编——计算斐波那契数列程序（详细注释和流程图说明）

X86汇编实现斐波那契数列

程序说明：

输入斐波那契数列的项数， 然后依次输出斐波那契数列, 输入的项数小于256且为数字， 计算的项数不能超过2^16次方， 输入失败是 不会回显数字

因为存结果是AX， 只有16位， 最大为2^16 = 65536，所以程序设置当输入过大时, 只会显示项数小于 65536前的项数

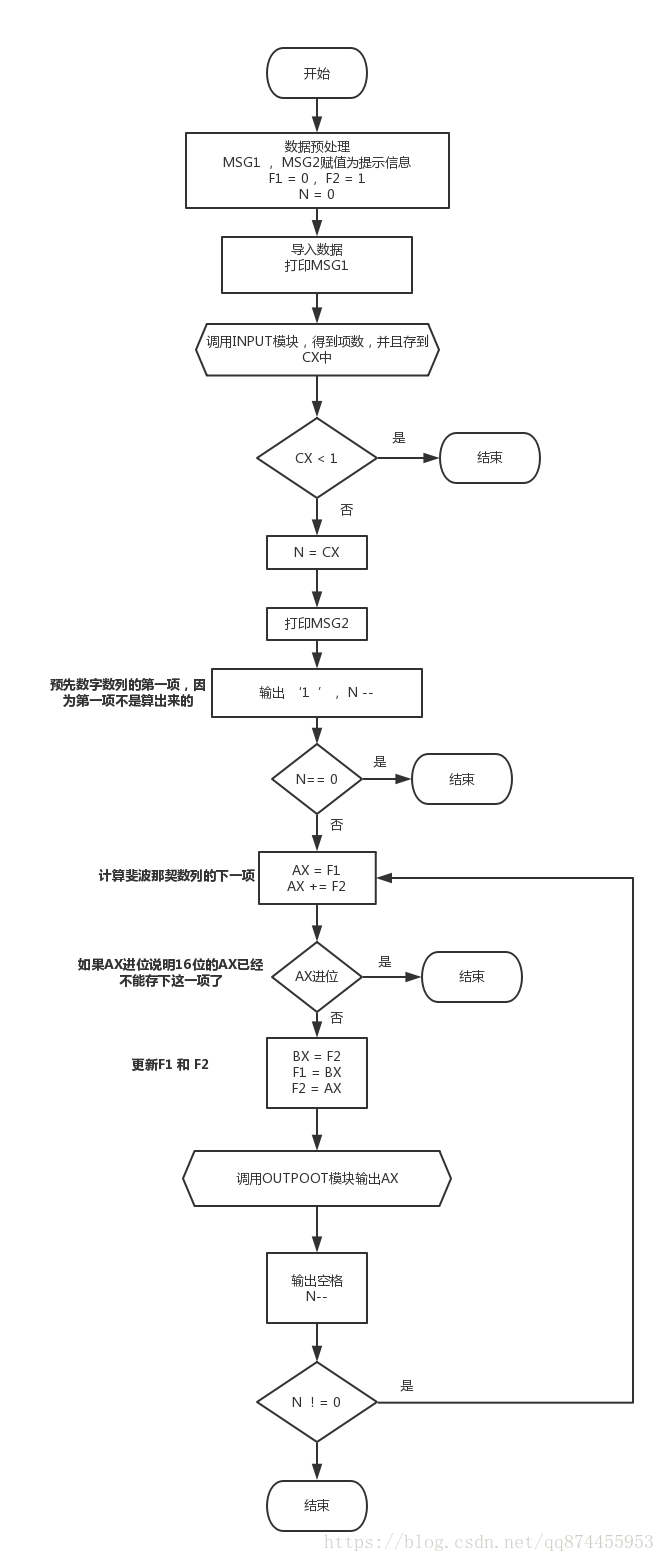
下面是程序的流程图

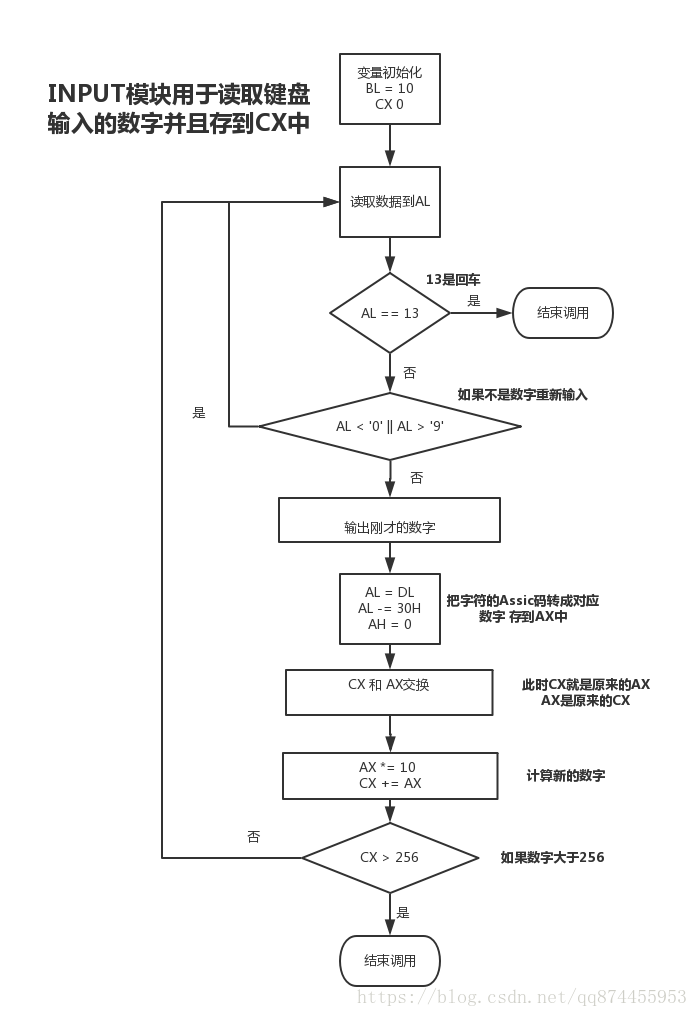
程序包括3个模块， 分别是主模块， INPUT模块（读取键盘中输入的合法数字）， OUTPUT模块（输出数字）

主模块

INPUT模块

OUTPUT模块

代码及其详细注释

ASSUME CS:CODE,DS:DATA
DATA SEGMENT
 MSG1 DB 13,10,'Please input the num of Fibonacci，no lager than 256 ， N =  $'
 MSG2 DB 13,10,'Fibonacci Sequence is: $'    ;提示信息

 N DW 0
 F1  DW 0
 F2  DW 1  ;计算数列的两个加数
DATA ENDS
;
CODE SEGMENT
START:
 MOV AX,DATA
 MOV DS,AX  ;导入数据
;
 LEA DX,MSG1
 MOV AH,9
 INT 21H    ;打印提示信息1

 CALL INPUT ;调用INPUT模块， 得到项数 存到 CX中

 CMP CX,1    ;如果CX < 1 输入不合法
 JB EXIT     ;直接退出   

 MOV N,CX     ;令N = CX  即 N为数列项数

 LEA DX,MSG2    ;打印输出信息 ‘Fibonacci Sequence is:’
 MOV AH,9     ;调用的是9号方法 .09H号调用，字符串输出显示
 INT 21H

;先处理第一个项
 MOV DL,'1'  ; 先把 1 放到输出区
 MOV AH,2
 INT 21H
 MOV DL,' '
 INT 21H     ; 输出 1 和 空格
 DEC N       ; N --;
 JZ EXIT     ; 当 N = 0时，退出

LOOP:
 MOV AX,F1   ; 把 AX = F1
 ADD AX,F2   ; AX =+ F2
 JC EXIT     ; AX发生进位 即 AX不能表示数字
 MOV BX,F2
 MOV F1,BX   ;不能 直接MOV F1,F2 不支持这样做
 MOV F2,AX   ; 把 F2 赋值给 F1 , AX （计算出来的一项） 赋值给 F2
 CALL OUTPUT ; 调用输出模块 输出计算的项
 MOV DL,' '
 MOV AH,2
 INT 21H     ;输出空格
 DEC N       ; N--
 JNZ LOOP    ;跳转到循环LOOP JNZ是由标志位ZF  而ZF是算术运算可以改变的，
             ;这里可能使ZF发生改变的是上一个指令    DEC N  ， 当N ！= 0 条件成立
EXIT:
 MOV AH,4CH
 INT 21H    ;退出程序
;
INPUT:
 MOV BL,10 ;  BL 为 10
 MOV CX,0  ;  CX 为 0

IN_X:       ;输入数字  

 MOV AH,7
 INT 21H     ;读取数据 

 CMP AL,13 ; 读取的字符是 回车
 JE IN_END ; 跳转到输入结束模块  

 CMP AL,'0' ; 输入不合法 就继续输入
 JB IN_X
 CMP AL,'9' ; 输入不合法 就继续输入
 JA IN_X  

 MOV DL,AL  ;把合法数字 存入到DL  

 MOV AH,2    ; 调用2号功能 输出刚才输入的字符
 INT 21H
 MOV AL,DL
 SUB AL,30H  ; 把assic码变成数字
 MOV AH,0    ; AH 为 0
 XCHG AX,CX  ; 把cx变成刚输入的数字
 MUL BL      ; AX = AL * BL(10) 也就是乘以相应的权 百位数乘100  十位数乘10
 ADD CX,AX   ; CX += AX;   cx表示的就是真正输入的斐波那契项数
 ;这里设置项数的最大值， 项数最大为256 如果输入大于256 就直接结束
 CMP CH,0    ;判断CX的前8位是不是为0， 如果不为0， 说明大于256
 JNZ IN_END  ;大于256 直接结束输入
 JMP IN_X    ;否则继续输入

IN_END:
 RET   ;结束调用
;
OUTPUT:
 MOV BX,10  ;BX 初始化为 10
 MOV CX,0   ;CX 初始为 0
;会接着运行下面的代码
; 下面的代码用于把数字转换成字符串
;方法是每次把数除10 得到余数 压入栈中在，直到被除数为0， 然后依次输出栈顶字符       

LOOP1:MOV DX,0  ;  DX = 0
 DIV BX       ; AX为被除数 AX =  AX / 10;  余数放在DX里 ，这就是最低位的数字
 ADD DL,'0'   ; 把DL 加上 '0'  此时 DL是能直接输出的字符数字
 PUSH DX      ; 把DX 压入栈
 INC CX       ; CX ++
 CMP AX,0
 JNZ LOOP1      ; 如果AX 不为 0, 就继续LOOP1
 MOV AH,2
LOOP2:POP DX    ;循环输出栈的字符
 INT 21H
 LOOP LOOP2
 RET          ;结束调用
;
CODE ENDS
 END START