5.13 省选模拟赛 优雅的绽放吧,墨染樱花 多项式 prufer序列 计数 dp

LINK：优雅的绽放吧,墨染樱花

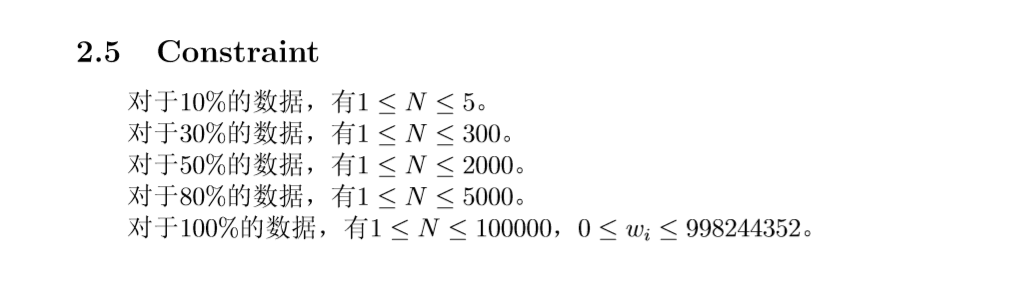
当时考完只会50分的做法 最近做了某道题受到启发 故会做这道题目了。(末尾附30分 50分 100分code

看到度数容易想到prufer序列 考虑dp统计方案数。

设f[i][j]表示前i个数字占了prufer序列j个位置的方案数.最后答案为f[n][n-2].

容易想到转移 \(f[i][j]+=f[i-1][k]\cdot C(n-k,j-k)\cdot w_i^{j-k+1}\cdot (j-k+1)\)

复杂度n^3 期望得分30.

容易发现第二维是一个卷积 NTT优化 复杂度n^2log 期望得分50.

考虑满分做法：若知道一个度数排列 满足\(\sum_i d_i=n-2\)

那么容易计算出贡献. 贡献为\(\frac{(n-2)!}{\Pi (d_i!)}\Pi (d_i+1)w_i^{d_i+1}\)

考虑对于这个式子先进行化简:\((n-2)!\Pi w_i\frac{1}{\Pi (d_i!)}\Pi (d_i+1)w_i^{d_i}\)

那么前面是一个常数 考虑对后面的式子进行变形.

由于存在阶乘 考虑设出EGF来解决问题。

对于第i个点 设F(x)为其贡献的EGF. \(F(x)=\sum_{j=0}^{\infty}\frac{w_i^{j}x^j(j+1)}{j!}\)

那么我们要求的就是 \([x^{n-2}]\Pi F(x_i)\)

直接求复杂度还是n^2log 这个连乘很麻烦 考虑化简.

考虑取对数 然后再exp回来 逐个取复杂度还是很高。

一个trick 设\(G(x)=\sum_{j=0}^{\infty}\frac{x^j(j+1)}{j!}\)

那么对G(x)取对数后对应项乘以 \(w_i^k\) 那么和刚才的F(x)取对数等价。

关键如何求\(\sum_{k=0}\sum_{i=1}^n w_i^k\)

还是设出上式的生成函数W(x) 容易得到\(W(x)=\sum_{i=1}^n\frac{1}{1-w_ix}\)

\(W(x)=\sum_{i=1}^n1-\frac{w_ix}{1-w_ix}\)

一个trick \([Ln(1-w_ix)]'=-\frac{w_i}{1-w_ix}\)

此时有 \(W(x)=n-x\sum_{i=1}^n(Ln(1-w_ix))\)

那么存在\(W(x)=n-x(Ln(\Pi_{}^n(1-w_ix)))'\)

里面那个东西可以直接分治NTT求.

综上分为两部 前者nlogn 后者 nlog^2. 期望得分100.

score 30
const int MAXN=5010;
int n;
int w[MAXN],fac[MAXN],inv[MAXN];
int f[MAXN][MAXN];//f[i][j]表示前i个数填了j个位置的贡献.
inline int ksm(int b,int p)
{
	int cnt=1;
	while(p){if(p&1)cnt=(ll)cnt*b%mod;p=p>>1;b=(ll)b*b%mod;}
	return cnt;
}
inline int C(int a,int b){if(a<b)return 0;return (ll)fac[a]*inv[b]%mod*inv[a-b]%mod;}
int main()
{
	freopen("yuyuko.in","r",stdin);
    freopen("yuyuko.out","w",stdout);
	get(n);fac[0]=1;
	rep(1,n,i)get(w[i]),fac[i]=(ll)fac[i-1]*i%mod;
	inv[n]=ksm(fac[n],mod-2);
	fep(n-1,0,i)inv[i]=(ll)inv[i+1]*(i+1)%mod;
	f[0][0]=1;
	rep(1,n,i)
	{
		rep(0,n-2,j)
		{
			int ww=1;
			rep(1,j+1,k)
			{
				ww=(ll)ww*w[i]%mod;
				f[i][j]=(f[i][j]+(ll)f[i-1][j-k+1]*C(n-2-j+k-1,k-1)%mod*k%mod*ww)%mod;
			}
		}
	}
	put(f[n][n-2]);
	return 0;
}
score 50
const int MAXN=200010,G=3;
int n,lim,INV;
int w[MAXN],rev[MAXN],fac[MAXN],inv[MAXN];
int f[MAXN],g[MAXN],c[MAXN];//f[i][j]表示前i个数填了j个位置的贡献.
inline int ksm(int b,int p)
{
	int cnt=1;
	while(p){if(p&1)cnt=(ll)cnt*b%mod;p=p>>1;b=(ll)b*b%mod;}
	return cnt;
}
inline int C(int a,int b){if(a<b)return 0;return (ll)fac[a]*inv[b]%mod*inv[a-b]%mod;}
inline void NTT(int *a,int op)
{
	rep(1,lim-1,i)if(i<rev[i])swap(a[i],a[rev[i]]);
	for(int len=2;len<=lim;len=len<<1)
	{
		int mid=len>>1;
		int wn=ksm(G,op==1?(mod-1)/len:mod-1-(mod-1)/len);
		for(int j=0;j<lim;j+=len)
		{
			int d=1;
			for(int i=0;i<mid;++i)
			{
				int x=a[i+j],y=(ll)a[i+j+mid]*d%mod;
				a[i+j]=(x+y)%mod;a[i+j+mid]=(x-y+mod)%mod;
				d=(ll)d*wn%mod;
			}
		}
	}
}
int main()
{
	freopen("yuyuko.in","r",stdin);
    freopen("yuyuko.out","w",stdout);
	get(n);fac[0]=1;f[0]=1;
	rep(1,n,i)get(w[i]),fac[i]=(ll)fac[i-1]*i%mod;
	inv[n]=ksm(fac[n],mod-2);
	fep(n-1,0,i)inv[i]=(ll)inv[i+1]*(i+1)%mod;
	lim=1;while(lim<n-2+n-2+1)lim=lim<<1;
	rep(1,lim-1,i)rev[i]=rev[i>>1]>>1|((i&1)?lim>>1:0);
	INV=ksm(lim,mod-2);
	rep(1,n,i)
	{
		int ww=1;
		rep(0,n-2,j)
		{
			ww=(ll)ww*w[i]%mod;
			f[j]=(ll)f[j]*fac[n-2-j]%mod;
			g[j]=(ll)inv[j]*(j+1)%mod*ww%mod;
		}
		rep(n-1,lim-1,j)f[j]=0,g[j]=0;
		NTT(g,1);NTT(f,1);rep(0,lim-1,j)f[j]=(ll)f[j]*g[j]%mod;
		NTT(f,-1);rep(0,n-2,j)f[j]=(ll)f[j]*INV%mod*inv[n-2-j]%mod;
	}
	put(f[n-2]);
	return 0;
}
score 100
const int MAXN=300010,GG=3;
int n;
int w[MAXN],O[MAXN],rev[MAXN],f[MAXN],g[MAXN];
int fac[MAXN],inv[MAXN],C[MAXN],D[MAXN],ans[MAXN];
int A[20][MAXN],tv[MAXN],v[MAXN],E[MAXN],F[MAXN],G[MAXN];
inline int ksm(int b,int p)
{
	int cnt=1;
	while(p)
	{
		if(p&1)cnt=(ll)cnt*b%mod;
		b=(ll)b*b%mod;p=p>>1;
	}
	return cnt;
}
inline void NTT(int *a,int op,int lim)
{
	rep(1,lim-1,i)
	{
		rev[i]=rev[i>>1]>>1|((i&1)?lim>>1:0);
		if(i<rev[i])swap(a[i],a[rev[i]]);
	}
	for(int len=2;len<=lim;len=len<<1)
	{
		int mid=len>>1;
		int wn=ksm(GG,op==1?(mod-1)/len:mod-1-(mod-1)/len);
		rep(1,mid-1,i)O[i]=(ll)O[i-1]*wn%mod;
		for(int j=0;j<lim;j+=len)
		{
			for(int i=0;i<mid;++i)
			{
				int x=a[i+j],y=(ll)a[i+j+mid]*O[i]%mod;
				a[i+j]=(x+y)%mod;a[i+j+mid]=(x-y+mod)%mod;
			}
		}
	}
	if(op==-1)for(int i=0,INV=ksm(lim,mod-2);i<=lim-1;++i)a[i]=(ll)a[i]*INV%mod;
}
inline void solve(int l,int r,int d)
{
	if(l==r)return A[d][0]=1,A[d][1]=mod-w[l],void();
	int mid=(l+r)>>1;
	solve(l,mid,d);solve(mid+1,r,d+1);
	int lim=1;while(lim<=r-l+1)lim=lim<<1;
	rep(mid-l+2,lim-1,i)A[d][i]=0;
	rep(r-mid+1,lim-1,i)A[d+1][i]=0;
	NTT(A[d],1,lim);NTT(A[d+1],1,lim);
	rep(0,lim-1,i)A[d][i]=(ll)A[d][i]*A[d+1][i]%mod;
	NTT(A[d],-1,lim);
}
inline void Direv(int *A,int *B,int len)
{
	rep(1,len-1,i)B[i-1]=(ll)A[i]*i%mod;B[len-1]=0;
}
inline void Inv(int *A,int *B,int len)
{
	if(len==1)return B[0]=ksm(A[0],mod-2),void();
	Inv(A,B,len>>1);rep(0,len-1,i)E[i]=A[i],F[i]=B[i];
	NTT(E,1,len<<1);NTT(F,1,len<<1);
	rep(0,(len<<1)-1,i)E[i]=(ll)E[i]*F[i]%mod*F[i]%mod;
	NTT(E,-1,len<<1);
	rep(0,len-1,i)B[i]=((ll)2*B[i]-E[i]+mod)%mod;
	rep(0,(len<<1)-1,i)E[i]=F[i]=0;
}
inline void Inter(int *A,int *B,int len)
{
	rep(1,len-1,i)B[i]=(ll)A[i-1]*inv[i]%mod*fac[i-1]%mod;B[0]=0;
}
inline void Ln(int *A,int *B,int len)
{
	Direv(A,C,len);Inv(A,D,len);
	NTT(C,1,len<<1);NTT(D,1,len<<1);
	rep(0,(len<<1)-1,i)C[i]=(ll)C[i]*D[i]%mod;
	NTT(C,-1,len<<1);Inter(C,B,len);
	rep(0,(len<<1)-1,i)C[i]=D[i]=0;
}
inline void Exp(int *A,int *B,int len)
{
	if(len==1)return B[0]=1,void();
	Exp(A,B,len>>1);Ln(B,G,len);
	G[0]=(A[0]+1-G[0]+mod)%mod;
	rep(1,len-1,i)G[i]=(A[i]-G[i]+mod)%mod;
	NTT(B,1,len<<1);NTT(G,1,len<<1);
	rep(0,(len<<1)-1,i)B[i]=(ll)B[i]*G[i]%mod;
	NTT(B,-1,len<<1);
	rep(len,(len<<1)-1,i)B[i]=G[i]=0;
}
int main()
{
	freopen("yuyuko.in","r",stdin);
    freopen("yuyuko.out","w",stdout);
	get(n);
	if(n==1){puts("0");return 0;}
	rep(1,n,i)get(w[i]);
	//先求出G(x)=1+ai^kx^k;
	int len=1;fac[0]=1;O[0]=1;
	while(len<=n)len=len<<1;
	rep(1,(len<<1),i)fac[i]=(ll)fac[i-1]*i%mod;
	inv[len<<1]=ksm(fac[len<<1],mod-2);
	fep((len<<1)-1,0,i)inv[i]=(ll)inv[i+1]*(i+1)%mod;
	solve(1,n,0);rep(0,n,i)tv[i]=A[0][i];
	Ln(tv,v,len);v[0]=n;
	rep(1,len-1,i)v[i]=mod-(ll)v[i]*i%mod;
	rep(0,len-1,i)f[i]=(ll)inv[i]*(i+1)%mod;
	Ln(f,g,len);
	rep(0,len-1,i)g[i]=(ll)g[i]*v[i]%mod;
	Exp(g,ans,len);
	int res=(ll)ans[n-2]*fac[n-2]%mod;
	rep(1,n,i)res=(ll)res*w[i]%mod;
	put(res);return 0;
}