三节课MINI计划第五周
一、任务及干货

二、作品
(一)小组分工
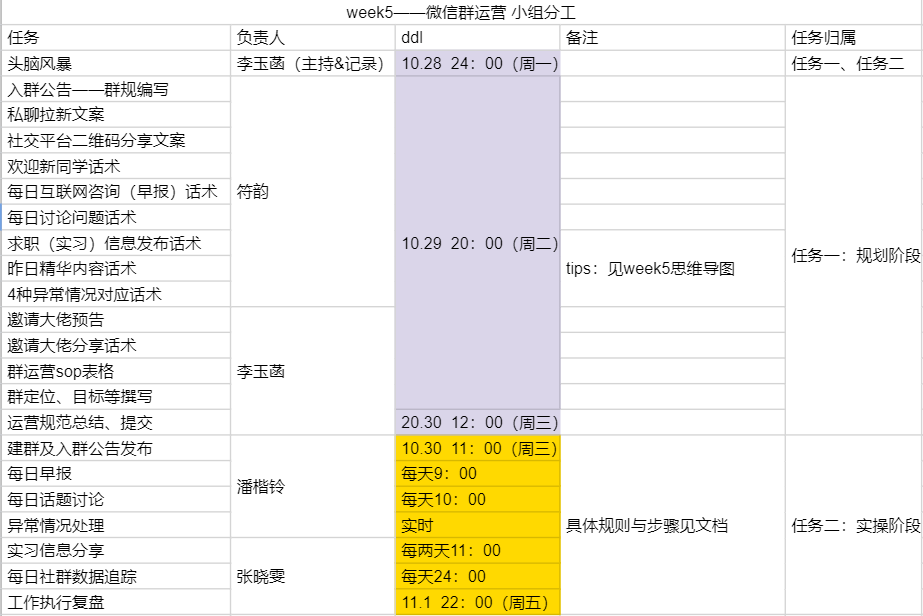
(二)社群运营方案

三节课MINI计划第五周的更多相关文章
- 三节课MINI计划第三周
第一部分 微信读书的产品分析 一.任务背景 二.做什么 三.TASK8 业务流程图 四.TASK9 五.周会 六.周报
- 三节课MINI计划第一周
第一部分 产品经理做什么以及需要的能力 (一)用户分析 用户群——行为分析——需求痛点——产品卖点——更多用户群 (二)功能分析 产品调研——产品结构——功能点——关键流程——下一轮产品调研 (三 ...
- 三节课MINI计划第二周
任务:完成一份用户反馈的收集,并进行分析 第一步:去你能想到的公开.非公开渠道收集最近90天,至少40条和B站相关的有效用户差评反馈,并根据你对业务的理解分类整理,以表格的形式进行整理,以图片的方式提 ...
- 三节课MINI计划第四周
一.任务 二.任务一 (一)梳理产品卖点 (二)策划线上活动 三.任务二 四.周报
- ARTS打卡计划第五周
Algorithms: https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/ 采用了map的 ...
- # 第五周课下测试(ch03)补交
第五周课下测试(ch03)补交 1.( 多选题 | 1 分) 有关gdb调试汇编,下面说法正确的是() A . 可以用disas反汇编当前函数 B . 以16进制形式打印%rax中内容的命令是 pri ...
- 2018-2019-20172329 《Java软件结构与数据结构》第五周学习总结
2018-2019-20172329 <Java软件结构与数据结构>第五周学习总结 教材学习内容总结 <Java软件结构与数据结构>第九章-排序与查找 一.查找 1.查找概念简 ...
- 20155320 2016-2017-2 《Java程序设计》第五周学习总结
20155320 2016-2017-2 <Java程序设计>第五周学习总结 教材学习内容总结 错误处理 java中所有错误都会被打包为对象,可以通过try catch 代表错误的对象后做 ...
- “Hello World!”团队第五周第六次会议
“Hello World!”团队第五周第六次会议 博客内容: 一.会议时间 二.会议地点 三.会议成员 四.会议内容 五.todo list 六.会议照片 七.燃尽图 八.checkout& ...
随机推荐
- IntelliJ IDEA——数据库集成工具(Database)的使用
https://www.cnblogs.com/huiyi0521/p/10125537.html idea集成了一个数据库管理工具,可以可视化管理很多种类的数据库,意外的十分方便又好用.这里以ora ...
- 十五.DNS子域授权、分离解析、缓存DNS服务器
1.搭建基本DNS服务器 pc7: 1.1 安装软件包 ]# yum -y install bind-chroot bind bind //域名服务包 bind-chroot //提 ...
- [GXOI/GZOI2019]特技飞行
题目链接 [https://www.luogu.org/problem/P5302] 思路:这道题可以说是两道题的合并.注意到\(c\)的分数与 \(a\)和\(b\)的分数 无关,也就是说可以分成两 ...
- Elasticsearch-head使用及ES相关概念
elasticsearch-head安装和介绍已在上一篇讲了. 在浏览器访问http://localhost:9100,可看到如下界面,表示启动成功: 仔细观察,我们会发现客户端默认连接的是我们ela ...
- xlrd/xlwt
操作 xls格式的excel文件 读模块 xlrd import xlrd 打开文件 wb= xlrd.open_workbook('xxxx.xls') 获取excel中的表 ws= wb.shee ...
- django项目部署上线 nginx + uwsgi
一.安装python3 安装步骤:https://www.cnblogs.com/zhangqigao/p/11661875.html 二.修改django中的配置文件 修改settings.py ( ...
- Readiness probe failed:connection refused
我的K8S集群在启动一个POD的时候说死起不来,然后就报下面的错误 Events: Type Reason Age From Message ---- ------ ---- ---- ------- ...
- VTK 简单点云数据显示绘制
基于vtkPolyData,绘制时除了输入点坐标,还需要通过setVerts指定点绘制信息. simplePoints.txt的内容为简单的 xyz,如: 20 20 20 20 20 30 20 2 ...
- 关于解决ruby源码安装 gem install报错问题
因做redis集群需要安装ruby,源码安装过后gem install redis安装redis接口报错 解决方案: 确保主机安装zlib,没有安装执行 yum -y install zlib zli ...
- Codeforces - 2019年11月补题汇总
大概目标是补到 #500 为止的 Div. 2 ,先定个小目标,寒假开始前补到 #560 为止 Codeforces Round #599 (Div. 2) 5/6 备注:0-1BFS(补图连通块) ...
