Codeforces Round #599 (Div. 2) A,B1，B2,C 【待补 D】

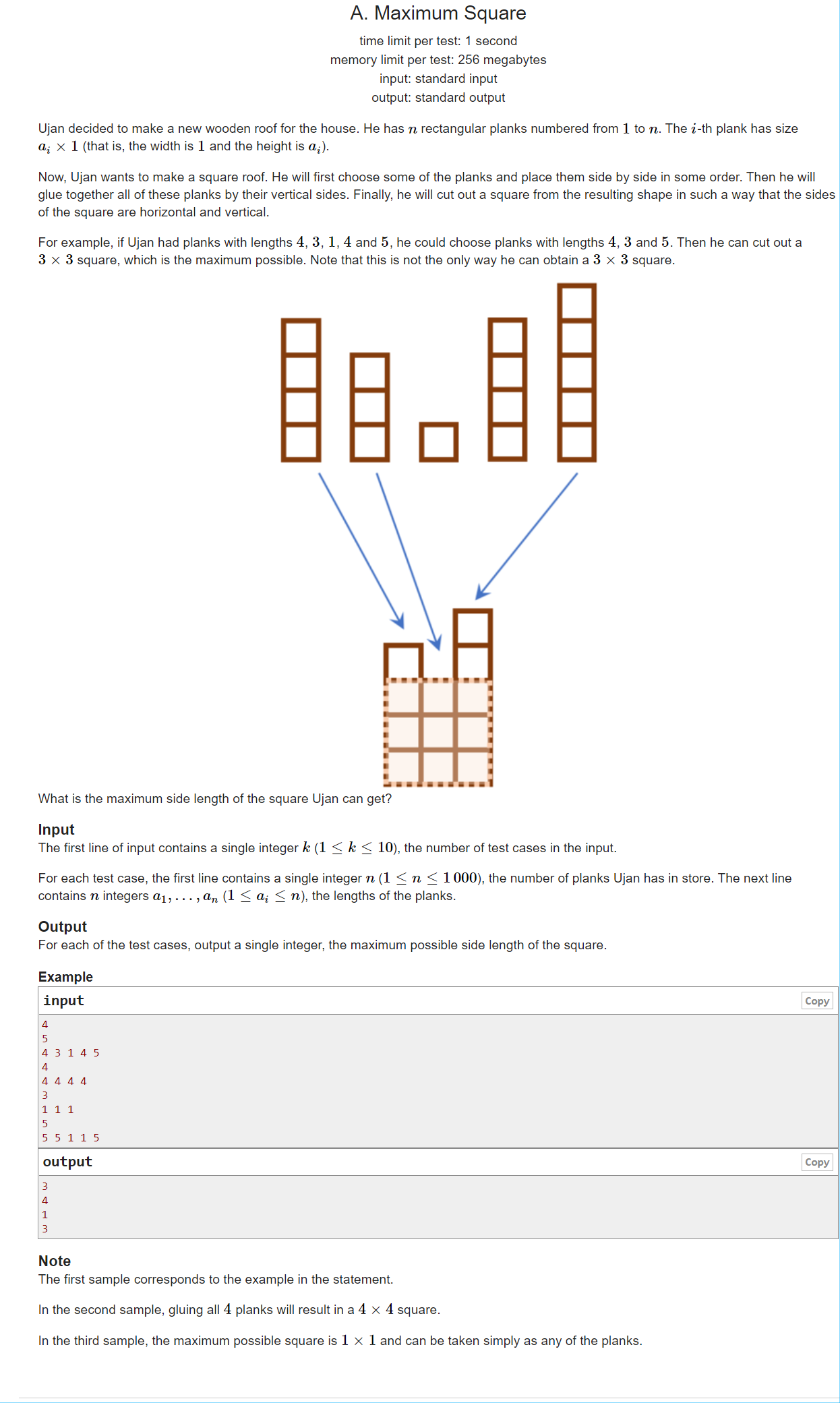
排序+暴力

 #include<bits/stdc++.h>

 using namespace std;

 #define int long long
 #define N 1005000
 int arr[N];

 signed main(){
     int _,n;
     cin>>_;
     while(_--){
         cin>>n;
         for(int i=;i<=n;i++)
             cin>>arr[i];
         sort(arr+,arr++n);
         int ans=;
         for(int i=;i<=n;i++){
             int flag=;
             int s=;
             for(int j=n;j>=;j--){
                 if(arr[j]>=i)
                     s++;
                 if(s>=i){
                     flag=;
                     break;
                 }
             }
             if(flag){
                 ans=i;
             }else{
                 break;
             }
         }
         cout<<ans<<'\n';
     }
     return ;
 }

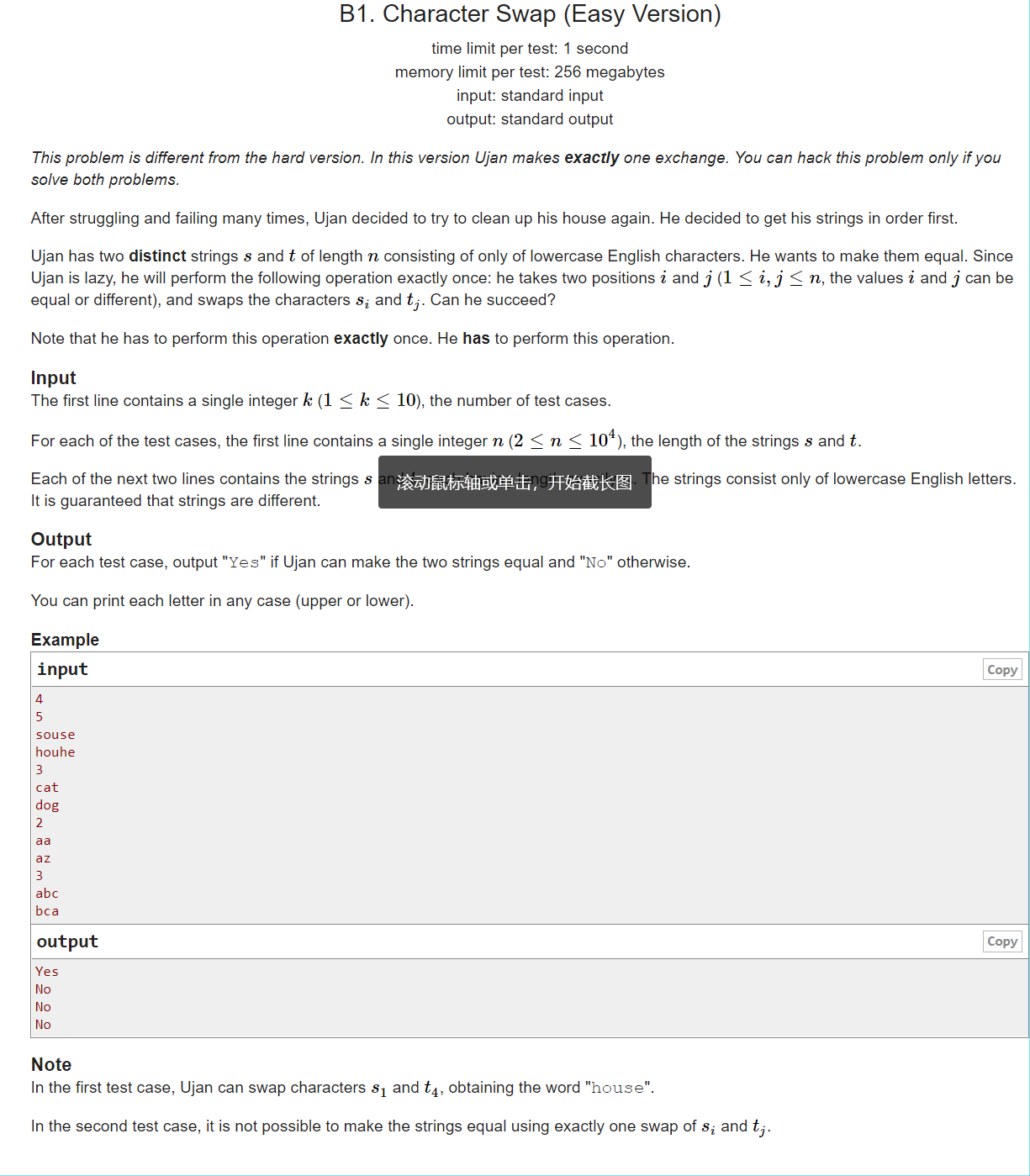
直接暴力就行。【数据范围看错了。少开了一个0。啊啊，难受QAQ。。。。。。。】

 #include<bits/stdc++.h>

 using namespace std;

 #define int long long
 #define N 1500
 int a[N];
 signed main(){
     int _;
     cin>>_;
     while(_--){
         int n;
         cin>>n;
         string s1,s2;
         cin>>s1>>s2;
         if(s1==s2){
             printf("Yes\n");
             continue;
         }
         int flag=;int s=;

         memset(a,,sizeof(a));
          int cnt=;
         for(int i=;i<s1.size();i++){
             if(s1[i]!=s2[i]){
                 a[cnt++]=i;
                 s++;
             }
             if(s>){
                 break;
             }
         }
         if(s!=){
             printf("No\n");
         }else{
             if((s1[a[]]==s1[a[]]&&s2[a[]]==s2[a[]])){
                 printf("Yes\n");
             }else{
                 printf("No\n");
             }
         }
     }
     return ;
 }

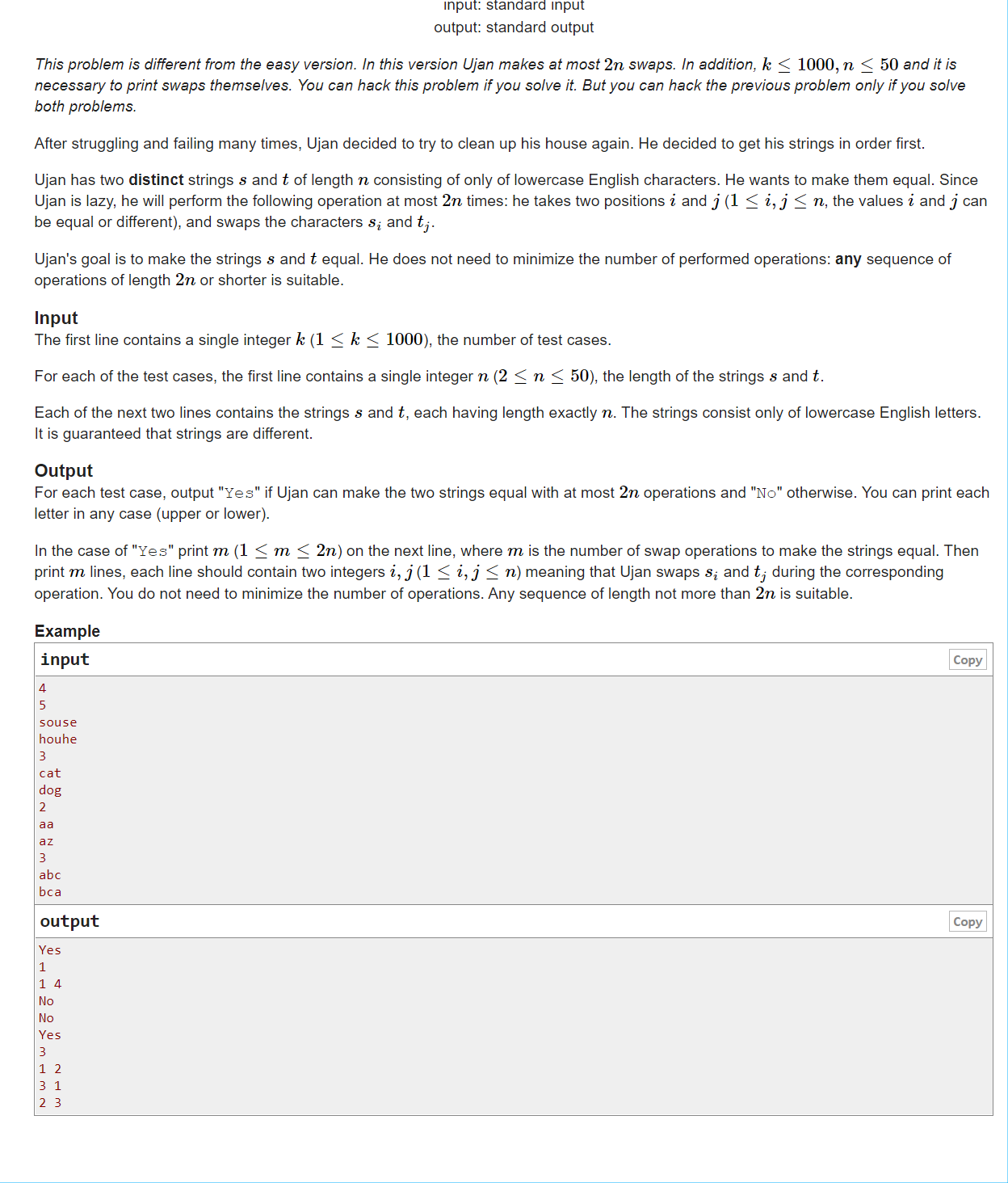
思路：当字符串不相等时，优先考虑同行。当同行没有字符串时再考虑另外一行。模拟即可。

 #include<bits/stdc++.h>

 using namespace std;
 #define int long long

 signed main(){
     int _;
     cin>>_;
     while(_--){
         int n;
         cin>>n;
         string s1,s2;
         cin>>s1>>s2;
         int sum=;int X=;
         vector<pair<int,int> > ans;
         for(int i=;i<n;i++){
             if(s1[i]!=s2[i]){
                 int flag1=;int flag2=;
                 for(int j=i+;j<n;j++){
                     if(s1[j]==s1[i]){
                         flag1=;
                         sum++;
                         ans.push_back(make_pair(j+,i+));
                         swap(s1[j],s2[i]);
                         break;
                     }
                 }
                 if(!flag1){
                     for(int j=i+;j<s2.size();j++){
                         if(s2[j]==s1[i]){
                             sum+=;
                             flag2=;
                             ans.push_back(make_pair(j+,j+));
                             ans.push_back(make_pair(j+,+i));
                             swap(s2[j],s1[j]);
                             swap(s1[j],s2[i]);
                             break;
                         }
                     }
                 }
                 if(flag1==&&flag2==){
                     X=;
                     break;
                 }
             }
         }
         if(X){
             printf("No\n");
             continue;
         }
         if(sum<=*n){
             printf("Yes\n");
             printf("%lld\n",sum);
             for(int i=;i<ans.size();i++){
                 cout<<ans[i].first<<" "<<ans[i].second<<'\n';
             }
         }else{
             printf("No\n");
         }
     }
     return ;
 } 

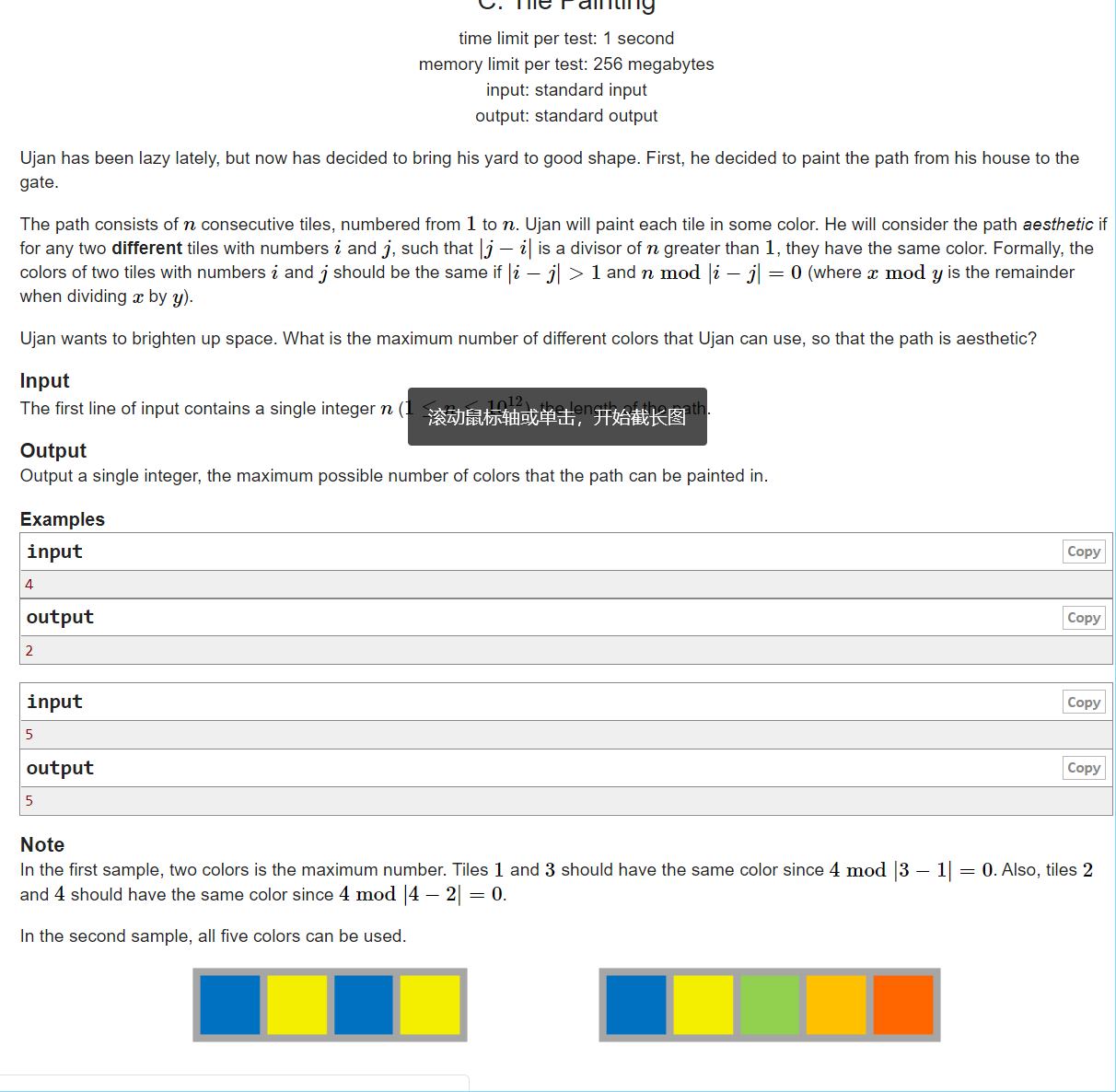
题意：给排成一行的 n个格子，要求所有的 i,j 满足 |i−j|是 n 的因子的，都要同色，求最大的涂色数。

思路：所有因子的GCD。

 #include<bits/stdc++.h>

 using namespace std;

 #define int long long

 signed main(){
     int n;cin>>n;
     int ans=;
     int flag=;
     int K=;
     for(int i=;i*i<=n;i++){
         if(n%i==){
             flag=;
             if(!K){
                 ans=i;
                 ans=__gcd(ans,n/i);
                 K=;
             }else{
                 ans=__gcd(ans,i);
             ans=__gcd(ans,n/i);
             }
         }
     }
     if(flag==){
         cout<<n<<'\n';
         return ;
     }
     cout<<ans;
     return ;
 }

菜是原罪。