BPTT

RNN 的 BP —— Back Propagation Through Time.

参考：零基础入门深度学习(5) - 循环神经网络。知乎。

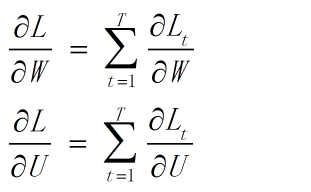
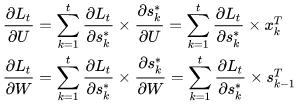
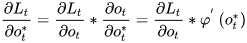
 1　　　def backward(self, sensitivity_array,
                  activator):
         '''
         实现BPTT算法
         '''
         self.calc_delta(sensitivity_array, activator)
         self.calc_gradient()
     def calc_delta(self, sensitivity_array, activator):
         self.delta_list = []  # 用来保存各个时刻的误差项
         for i in range(self.times):
             self.delta_list.append(np.zeros(
                 (self.state_width, 1)))
         self.delta_list.append(sensitivity_array)
         # 迭代计算每个时刻的误差项
         for k in range(self.times - 1, 0, -1):
             self.calc_delta_k(k, activator)
     def calc_delta_k(self, k, activator):
         '''
         根据k+1时刻的delta计算k时刻的delta
         '''
         state = self.state_list[k+1].copy()
         element_wise_op(self.state_list[k+1],
                     activator.backward)
         self.delta_list[k] = np.dot(
             np.dot(self.delta_list[k+1].T, self.W),
             np.diag(state[:,0])).T
     def calc_gradient(self):
         self.gradient_list = [] # 保存各个时刻的权重梯度
         for t in range(self.times + 1):
             self.gradient_list.append(np.zeros(
                 (self.state_width, self.state_width)))
         for t in range(self.times, 0, -1):
             self.calc_gradient_t(t)
         # 实际的梯度是各个时刻梯度之和
         self.gradient = reduce(
             lambda a, b: a + b, self.gradient_list,
             self.gradient_list[0]) # [0]被初始化为0且没有被修改过
     def calc_gradient_t(self, t):
         '''
         计算每个时刻t权重的梯度
         '''
         gradient = np.dot(self.delta_list[t],
             self.state_list[t-1].T)
         self.gradient_list[t] = gradient

 class RNN2(RNN1):
     # 定义 Sigmoid 激活函数
     def activate(self, x):
         return 1 / (1 + np.exp(-x))

     # 定义 Softmax 变换函数
     def transform(self, x):
         safe_exp = np.exp(x - np.max(x))
         return safe_exp / np.sum(safe_exp)

     def bptt(self, x, y):
         x, y, n = np.asarray(x), np.asarray(y), len(y)
         # 获得各个输出，同时计算好各个 State
         o = self.run(x)
         # 照着公式敲即可 ( σ'ω')σ
         dis = o - y
         dv = dis.T.dot(self._states[:-1])
         du = np.zeros_like(self._u)
         dw = np.zeros_like(self._w)
         for t in range(n-1, -1, -1):
             st = self._states[t]
             ds = self._v.T.dot(dis[t]) * st * (1 - st)
             # 这里额外设定了最多往回看 10 步
             for bptt_step in range(t, max(-1, t-10), -1):
                 du += np.outer(ds, x[bptt_step])
                 dw += np.outer(ds, self._states[bptt_step-1])
                 st = self._states[bptt_step-1]
                 ds = self._w.T.dot(ds) * st * (1 - st)
         return du, dv, dw

     def loss(self, x, y):
         o = self.run(x)
         return np.sum(
             -y * np.log(np.maximum(o, 1e-12)) -
             (1 - y) * np.log(np.maximum(1 - o, 1e-12))
         )