数据结构实验之图论八：欧拉回路（SDUT 3364）

Problem Description

在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。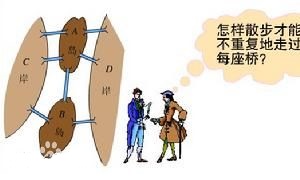



能否走过这样的七座桥，并且每桥只走一次？瑞士数学家欧拉最终解决了这个问题并由此创立了拓扑学。欧拉通过对七桥问题的研究，不仅圆满地回答了哥尼斯堡七桥问题，并证明了更为广泛的有关一笔画的三条结论，人们通常称之为欧拉定理。对于一个连通图，通常把从某结点出发一笔画成所经过的路线叫做欧拉路。人们又通常把一笔画成回到出发点的欧拉路叫做欧拉回路。具有欧拉回路的图叫做欧拉图。

你的任务是：对于给定的一组无向图数据，判断其是否成其为欧拉图？

---

Input

连续T组数据输入，每组数据第一行给出两个正整数，分别表示结点数目N(1 < N <= 1000)和边数M；随后M行对应M条边，每行给出两个正整数，分别表示该边连通的两个结点的编号，结点从1～N编号。

---

Output

若为欧拉图输出1，否则输出0。

---

Sample Input

1

6 10

1 2

2 3

3 1

4 5

5 6

6 4

1 4

1 6

3 4

3 6

---

Sample Output

1

---

Hint

如果无向图连通并且所有结点的度都是偶数，则存在欧拉回路，否则不存在。

题解：并查集就可以了，判断是否连通。也可以用BFS或者DFS来判断。 （懒得写了。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cstdlib>
using namespace std;
typedef long long ll;
int a[10005][1005];
int b[100005];
int found(int x)
{
    while(x!=b[x])
    {
        x = b[x];
    }
    return x;
}
void Merge(int x, int y)
{
    if(found(x) != found(y))
    {
        b[found(x)] = found(y);
    }
    return ;
}
int main()
{
    int t,n,m,u,v;
    scanf("%d",&t);
    while(t--)
    {
        memset(a, 0, sizeof(a));
        scanf("%d %d", &n, &m);
        for(int i = 0; i <= n; i ++)b[i] = i;    // 并查集初始化
        for(int i = 0; i < m; i ++)
        {
            scanf("%d %d", &u, &v);
            a[u][v] = a[v][u] = 1;   //用来判断度是否是偶数
            Merge(u,v);
        }
        int cnt = 0;
        for(int i = 1; i <= n; i ++)
        {
            if(b[i] == i) cnt ++;
        }
        if(cnt > 1) printf("0\n");   // 大于一说明不连通
        else
        {
            int f = 0;
            int sum = 0;
            for(int i = 1; i <= n; i ++)
            {
                sum = 0;
                for(int j = 1; j <= n; j ++)
                {
                    if(a[i][j] == 1)sum ++;
                }
                if(sum % 2 != 0)    // 一旦有的点的度数不是偶数，就不满足欧拉回路的条件了。
                {
                    f = 1;
                    break;
                }
            }
            if(f == 1) printf("0\n");
            else printf("1\n");
        }
    }
    return 0;
}