P2456 [SDOI2006]二进制方程

P2456 [SDOI2006]二进制方程

题解

拿个样例模拟一下发现

把等式两边对应展开，每个位置的填数都是一一对应的

比如第二个样例

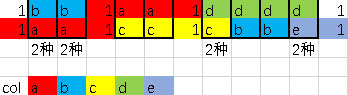
分类讨论：

（1）xi  yi  都是数字，但是不相同，此时无解

（2）xi  yi  都是数字，相同，唯一填法

（3）xi  yi  一个是数字，一个是字母，唯一填法

（4）xi  yi  都是字母，颜色不同，那么一旦在该颜色对应的位置上填了一个数字，对应的另一种颜色，或者是该颜色在其他区域的对应位置也填上了这个数字

所以我们就把同一种颜色的方块用并查集联系起来

解释代码：

（1）num[ ] 给0,1,每一个字母每一个位置都有唯一的编号，num[ i ]记录第 i 种字母的最后一个位置在哪里，但是实际应用起来就是下表对应的亚子：

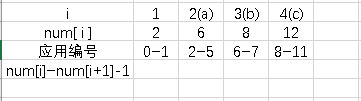
这么做是方便以后的并查集

（2）sum记录多少个待确定的位置（也就是有两种填法），答案其实是 2^{待确定位置数}

（3）x[ ] y[ ] 记录展开后的式子

（4）判断无解，1是x[  ] y[  ]长度不一样，2是 xi  yi 的祖先一个是1 一个是0

（5）取最大的一个的父亲是最小的一个

（6）高精度

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdlib>
#include<queue>

using namespace std;

inline int read()
{
    int ans=;
    char last=' ',ch=getchar();
    while(ch<''||ch>'') last=ch,ch=getchar();
    while(ch>=''&&ch<='') ans=ans*+ch-'',ch=getchar();
    if(last=='-') ans=-ans;
    return ans;
}

int num[],x[],y[],fa[],sum=,t1=,t2=,k;
char s[];
int c[],lenc;

int find(int x)
{
    return fa[x]==x?x:fa[x]=find(fa[x]);
}

void cheng()
{
    c[]*=;
    for(int i=;i<lenc;i++)
    {
        c[i]=c[i]*+c[i-]/;
        c[i-]%=;
    }
    while(c[lenc-]>=)
    {
        c[lenc]=c[lenc-]/;
        c[lenc-]%=;
        lenc++;
    }
}

int main()
{
    k=read();
    num[]=;  //解释1
    for(int i=,u;i<=k+;i++)
    {
        u=read();
        num[i]=num[i-]+u;
        sum+=u;  //解释2
    }
    scanf("%s",s);
    int len=strlen(s);
    for(int i=;i<len;i++)
    {
        if(s[i]>='a'&&s[i]<='z')
        {
            int v=s[i]-'a'+;
            for(int j=num[v];j<num[v+];j++) x[++t1]=j;
        }
        else x[++t1]=s[i]-'';
    }
    scanf("%s",s);
    len=strlen(s);
    for(int i=;i<len;i++)
    {
        if(s[i]>='a'&&s[i]<='z')
        {
            int v=s[i]-'a'+;
            for(int j=num[v];j<num[v+];j++) y[++t2]=j;
        }
        else y[++t2]=s[i]-'';
    }

    if(t1!=t2){ printf("0\n");return ; }  //无解判断 

    for(int i=;i<=num[k+];i++) fa[i]=i;

    for(int i=;i<=t1;i++)
    {
        int f1=find(x[i]),f2=find(y[i]);
        if(f1+f2==) { printf("0\n");return ; } //解释4
        if(f1!=f2)
        {
            fa[max(f1,f2)]=min(f1,f2);  //解释5
            sum--; //少了一个可以填两种方案的
        }
    }

    c[]=;lenc=;
    for(int i=sum;i>=;i--)
      cheng();  //解释6
    for(int i=lenc-;i>=;i--)
      printf("%d",c[i]);

    return ;
}