[PGM] Markov Networks

6 Markov Networks 系列

---

因果影响的独立性

noisy-or模型 和 广义线性模型

略，暂时不感兴趣。

---

Pairwise Markov Networks

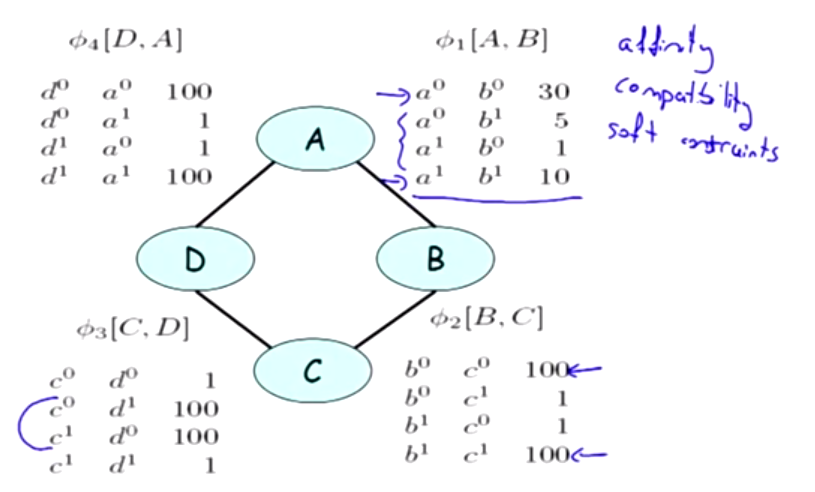
The last col is Happy value; [B,C]可见对课程的评价非常一致, they really agree with each other.

Markov Random Field 为何有归一化的问题，解释如下：

全连接网络，n个结点，每个结点有d种取值，那么parameter有多少个呢？

Gibbs distribution

6.Markov Network Fundamentals 

6.1 Pairwise Markov Network 

1. Pairwise 的 Markov Network各个相邻元素之间用Factor（Potential）来联系。
2. factor并不与概率成正比，因为真正的联合概率要受到其他与之联系的元素所影响。

6.2 General Gibbs Distribution 

1. Pairwise的network提供的信息远远无法表达整个网络里所有节点之间的概率关系。所以要引入Gibbs分布。
2. Gibbs分布由一些Factor组成。
3. Gibbs分布可以表达多个节点之间的联合概率（不只是pairwise的，可以是3个、4个一起）。Gibbs分布有能力表述整个网络里所有节点之间的概率关系。因为它至少可以用一个包含所有节点的Factor来表示。
4. Gibbs分布可以induce出Markov Network。
5. Induced Markov Network，就是把Gibbs分布的Factor里的节点都连起来。
6. 假设有一组Factor，做一下Factor product，然后归一化，求出所有元素的联合概率P。同时，这组Factor又可以induce出一个图H。那么P可以factorize over H。

6.3 Conditional Random Field 

1. CRF是MRF的一种变形，非常相似，但用处不同。CRF用来解决Task specific prediction。其实就是labelling problem。（好像MRF也是干这个的啊？）
2. CRF也是由一组Factor表示。看起来很像Gibbs分布的表示方式。但是它们的归一化方式不同，CRF把概率归一化成条件概率。
3. BN使用联合概率表示，它假设X1....Xn导致Y，而且各个X之间是独立的。如果各X之间不独立，则会出现Correlated feature，使概率的判断失真。而CRF使用条件概率表示，这样不管各X之间是否独立，都不会影响最后概率的判断。
4. CRF与logistics regression的关系。sigmoid函数也是一种CRF？？？

6.4 Independencies in Markov Network 

1. Separation in MN.只要active trail中的一个节点已知了，这个trail就断了。
2. 如果概率P factorizes over 图H，那么P也满足H表达出的independencies，所以H就是P的一个I-map。
3. 反过来，independency也可以推出factorization。假设有一个正分布P，H是它的一个I-Map，则P factorizes over 图H。

6.5 I-maps and perfect maps

1. P factorizes over G，则G是P的I-map。G表达了P中的某些independencies，但不一定是全部。
2. 最小I-map是指除了P中表达的independencies没有多余的路径的map。
3. Perfect map是指 I（G）= I（P），但是Perfect map不一定存在。
4. 这里Koller举了两个例子说明Perfect map有时候不存在，但是没怎么听懂。I-map必须是有向图？？P可以等效于无向图？？？
5. I-map也不是唯一的，不同的I-map可以表示相同的independencies，它们是I-equivalent的。多数的图都有很多I-equivalence。
6. BN和MN互相转换表示，会丢失independencies。

6.6 Log Linear Models

1. 把factor前面加log，本来factor product要做乘法，现在变成做加法。
2. Koller举了一个自然语言识别的例子,来说明我们可以用单词的feature来判断概率，而不是单词本身。
3. Ising model的例子，有点像用MRF做图像分割。温度高的时候原子之间的联系弱，温度低时联系强。但没明白她举这个例子想说明啥。这跟Log linear model有啥关系？
4. Metric MRFs。MRF可以提供局部平滑的假设，但首先我们要定义一个Metric，也就是定义MRF元素取值空间的距离函数。
5. 后面就讲了一些如何利用MRF做图像分割和图像去噪。这部分比较熟了。

6.7 Shared Feature in Log-Linear Model

1. 举了Ising model和NLP两个例子来说明有些条件（feature）是可以重复利用的。所以叫做Shared feature，这种feature对于所有的元素都适用。
2. 还是不明白这根log-linear model有啥关系。

7  Representation Wrap-up: Knowledge Engineering

7.1 Knowledge Engineering

1. 这部分讲的是关于技巧方面的内容，不太涉及理论。
2. Knowledge engineering有多种选择：基于模板的（图像分割）还是特殊设计的（医学诊断）？用有向图还是无向图？通用的（适合无label的数据，可以应对未知的数据）还是专用的（需要直接编写条件概率，可以人工简化高维的数据）？
3. Variable Types。网络中的变量有三类：目标变量，已观察到的变量，latent变量
4. Structure。要不要在网络中表达出因果关系。因果关系可以简化网络，使它更加直观。
5. Parameter：Value。手工建立网络时需要注意的问题。
6. Parameter：Local structure。这里讨论了几种网络的形式，但是没有具体例子，不是很明白。