mips体系堆栈回溯分析与实现

转载：http://www.sohu.com/a/118385096_468740

mips栈帧原理

Call stack 是指存放某个程序的正在运行的函数的信息的栈。Call stack 由 stack frames 组成，每个 stack frame 对应于一个未完成运行的函数。

在当今流行的计算机体系架构中，大部分计算机的参数传递，局部变量的分配和释放都是通过操纵程序栈来实现的。栈用来传递函数参数，存储返回值信息，保存寄存器以供恢复调用前处理机状态。 关于栈可见以前的文章： cdecl、stdcall、fastcall函数调用约定区别

每次调用一个函数，都要为该次调用的函数实例分配栈空间。为单个函数分配的那部分栈空间就叫做 stack frame，也就是说，stack frame 这个说法主要是为了描述函数调用关系的。

Stack frame 具体从2点来阐述

第一，它使调用者和被调用者达成某种约定。这个约定定义了函数调用时函数参数的传递方式，函数返回值的返回方式，寄存器如何在调用者和被调用者之间进行共享；

第二，它定义了被调用者如何使用它自己的 stack frame 来完成局部变量的存储和使用。

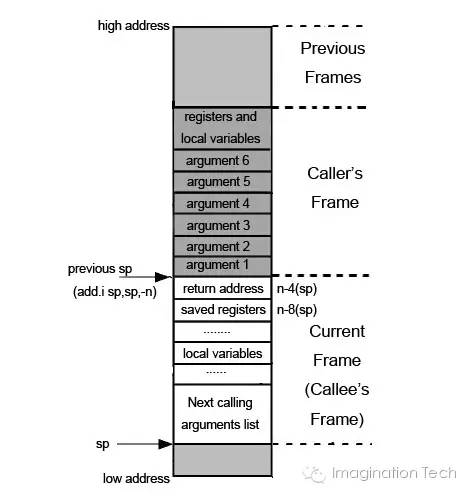
上图描述的是一种典型的(MIPS O32)嵌入式芯片的 stack frame 组织方式。在这张图中，计算机的栈空间采用的是向下增长的方式（intel 是确定向下增长的，arm可以配置栈增长方向，mips 是可配置还是只能向下增长？），SP(stack pointer) 就是当前函数的栈指针，它指向的是栈底的位置。Current Frame 所示即为当前函数(被调用者)的 frame ，Caller’s Frame 是当前函数的调用者的 frame 。

在没有 BP(base pointer) 寄存器的目标架构中，进入一个函数时需要将当前栈指针向下移动 n 字节，这个大小为n字节的存储空间就是此函数的 stack frame 的存储区域。此后栈指针便不再移动（在linux 内核代码 TODO 里面写着要加上在函数内部调整栈的考虑 – 虽然这通常不会发生），只能在函数返回时再将栈指针加上这个偏移量恢复栈现场。由于不能随便移动栈指针，所以寄存器压栈和出栈都必须指定偏移量，这与 x86 架构的计算机对栈的使用方式有着明显的不同。

RISC计算机一般借助于一个返回地址寄存器 RA(return address) 来实现函数的返回。几乎在每个函数调用中都会使用到这个寄存器，所以在很多情况下 RA 寄存器会被保存在堆栈上以避免被后面的函数调用修改，当函数需要返回时，从堆栈上取回 RA 然后跳转。移动 SP 和保存寄存器的动作一般处在函数的开头，叫做 function prologue；

注意如果当前函数是叶子函数（不存在对其它函数的调用，就不保存ra寄存器，反之就保存）。恢复这些寄存器状态的动作一般放在函数的最后，叫做 function epilogue。关于这些动作可以从IDA 反汇编的结果看出来：

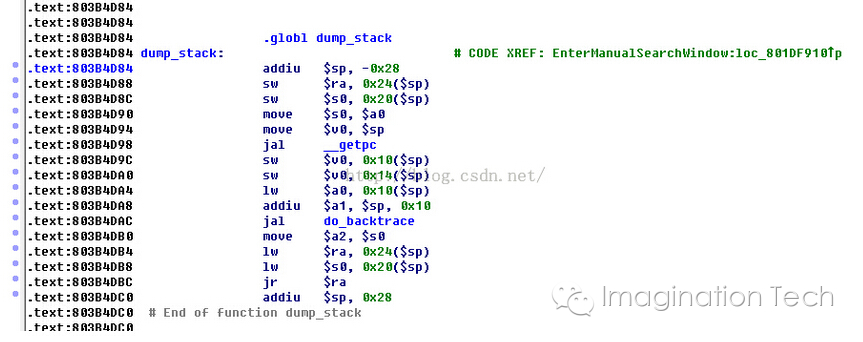
通过上面分析就有思路了：

首先获取当前的栈指针 sp，和指令指针 pc （也叫做 IP）

在mips下sp容易获取 已经约定$29 寄存器作为栈指针，所以可用如下内嵌汇编获取sp：

__asm__ volatile ("move %0, $29" : "=r"(reg));

MIPS没有记录当前PC地址的寄存器，就是说不能像ARM那样读PC寄存器。MIPS使用ra保存函数返回地址，利用这个特性可以获取到当前的PC。 比如：

#pragma GCC push_options

#pragma GCC optimize ("O0")

static unsigned int /*__attribute__((optimize("O0")))*/ * __getpc(void)

{

unsigned int *rtaddr;

__asm__ volatile ("move %0, $31" : "=r"(rtaddr));

return rtaddr;

}

#pragma GCC pop_options

对应的汇编代码是：

注意到上面代码中有 push_options 这是为了防止编译器偷偷把我们的代码给优化成 inline 了，那样就无法获取pc了。在要获取pc的地方调用就可以了：

pc = __getpc();

得到sp 和pc之后剩下的就开始回溯了，具体参考下面函数实现（linux 内核未修改代码，只加入注释）：

/*

* TODO for userspace stack unwinding:

* - handle cases where the stack is adjusted inside a function

* (generally doesn't happen)

* - find optimal value for max_instr_check

* - try to find a way to handle leaf functions

*/

static inline int unwind_user_frame(struct stackframe *old_frame,

const unsigned int max_instr_check) //// max_instr_check 函数最大可能的代码长度

{

struct stackframe new_frame = *old_frame;

off_t ra_offset = 0;

size_t stack_size = 0;

unsigned long addr;

if (old_frame->pc == 0 || old_frame->sp == 0 || old_frame->ra == 0)

return -9;

for (addr = new_frame.pc; (addr + max_instr_check > new_frame.pc) /// 上面通过 __getpc 获取的pc指针

&& (!ra_offset || !stack_size); --addr) {

union mips_instruction ip;

if (get_mem(addr, (unsigned long *) &ip)) /// 取出一条指令 ip

return -11;

if (is_sp_move_ins(&ip)) { /// 这条指令是不是 addiu $sp,imme 形式的

int stack_adjustment = ip.i_format.simmediate; /// 如果是求出 imme 立即数，那么本函数栈大小也就知道了

if (stack_adjustment > 0)

/* This marks the end of the previous function,

which means we overran. */

break;

stack_size = (unsigned long) stack_adjustment;

} else if (is_ra_save_ins(&ip)) { /// 是不是 sw / sd $ra, offset($sp) 类似的指令

int ra_slot = ip.i_format.simmediate; /// 如果是获取 offset

if (ra_slot < 0)

/* This shouldn't happen. */

break;

ra_offset = ra_slot;

} else if (is_end_of_function_marker(&ip))

break;

}

if (!ra_offset || !stack_size)

return -1;

if (ra_offset) {

new_frame.ra = old_frame->sp + ra_offset; /// 根据上面的 offset 和当前函数的sp指针得到存放 ra 数值的地址

if (get_mem(new_frame.ra, &(new_frame.ra))) /// 获取ra 的数值，也就是 jal func 这条指令所在的地址

return -13;

}

if (stack_size) {

new_frame.sp = old_frame->sp + stack_size; /// 上个函数的栈指针 貌似这里这么代码是错误的，反正我按我的方式改了能正确运行，

if (get_mem(new_frame.sp, &(new_frame.sp))) /// 这里这么写我也不懂。

return -14;

}

if (new_frame.sp > old_frame->sp)

return -2;

new_frame.pc = old_frame->ra;

*old_frame = new_frame;

return 0;

}

上面代码修改之后可以获取 上一层函数的 pc （jal func ：调用本函数的指令不就是上层函数的某一条指令？ ra 的值并不是jal func 的地址，而是jal func的地址 +8 ，传说中的 跳转延时槽）指针和sp 。

依此循环调用上面的函数一层层向上回溯，即可。