Codeforces Round #439 (Div. 2) Problem E (Codeforces 869E) - 暴力 - 随机化 - 二维树状数组 - 差分

Adieu l'ami.

Koyomi is helping Oshino, an acquaintance of his, to take care of an open space around the abandoned Eikou Cram School building, Oshino's makeshift residence.

The space is represented by a rectangular grid of n × m cells, arranged into n rows and m columns. The c-th cell in the r-th row is denoted by (r, c).

Oshino places and removes barriers around rectangular areas of cells. Specifically, an action denoted by "1 r1 c1 r2 c2" means Oshino's placing barriers around a rectangle with two corners being (r1, c1) and (r2, c2) and sides parallel to squares sides. Similarly, "2 r1 c1 r2 c2" means Oshino's removing barriers around the rectangle. Oshino ensures that no barriers staying on the ground share any common points, nor do they intersect with boundaries of the n × m area.

Sometimes Koyomi tries to walk from one cell to another carefully without striding over barriers, in order to avoid damaging various items on the ground. "3 r1 c1 r2 c2" means that Koyomi tries to walk from (r1, c1) to (r2, c2) without crossing barriers.

And you're here to tell Koyomi the feasibility of each of his attempts.

Input

The first line of input contains three space-separated integers n, m and q (1 ≤ n, m ≤ 2 500, 1 ≤ q ≤ 100 000) — the number of rows and columns in the grid, and the total number of Oshino and Koyomi's actions, respectively.

The following q lines each describes an action, containing five space-separated integers t, r1, c1, r2, c2 (1 ≤ t ≤ 3, 1 ≤ r1, r2 ≤ n, 1 ≤ c1, c2 ≤ m) — the type and two coordinates of an action. Additionally, the following holds depending on the value of t:

• If t = 1: 2 ≤ r1 ≤ r2 ≤ n - 1, 2 ≤ c1 ≤ c2 ≤ m - 1;
• If t = 2: 2 ≤ r1 ≤ r2 ≤ n - 1, 2 ≤ c1 ≤ c2 ≤ m - 1, the specified group of barriers exist on the ground before the removal.
• If t = 3: no extra restrictions.

Output

For each of Koyomi's attempts (actions with t = 3), output one line — containing "Yes" (without quotes) if it's feasible, and "No" (without quotes) otherwise.

Examples

input

5 6 5
1 2 2 4 5
1 3 3 3 3
3 4 4 1 1
2 2 2 4 5
3 1 1 4 4

output

No
Yes

input

2500 2500 8
1 549 1279 1263 2189
1 303 795 1888 2432
1 2227 622 2418 1161
3 771 2492 1335 1433
1 2017 2100 2408 2160
3 48 60 798 729
1 347 708 1868 792
3 1940 2080 377 1546

output

No
Yes
No

Note

For the first example, the situations of Koyomi's actions are illustrated below.

---

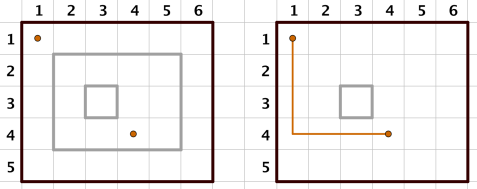
　　题目大意 在一个m×n的方格板上，操作1将一个矩形区域的边界上加上一圈障碍，操作2将一个矩形区域的边界上的障碍移除，操作3询问两点是否能不越过障碍互相到达。题目保证任意两圈矩形障碍不会有公共点(边界上)。

　　题目可以看成每次从平面中分割出一个小平面或者将一个平面复原，然后询问两个点是否在同一平面内。

　　于是常用套路打标记。

Solution 1 暴力差分

　　每次修改操作暴力每行进行差分。

　　当然这个差分得稍微改一下，前者用一个独一无二的正数，后者用一个负数。

　　查询的时候进行由那一行首往后扫描，如果遇到正数就压入栈，遇到负数就弹处栈顶。

　　最终栈顶就是这个点所在平面的标号。由于开始是在最外面的平面，所以首先在栈中加入一个元素。

　　然后判断一下两个点是否在同一平面就行了。

　　如果代码比较丑，请卡常数。

　　(最坏的时间复杂度是O(nq)，虽然觉得不可思议，但它就是过了。。)

Code

 /**
  * Codeforces
  * Problem#869E
  * Accepted
  * Time: 1934ms
  * Memory: 24600k
  */
 #include <bits/stdc++.h>
 using namespace std;

 int n, m, q;
 int top = ;
 int sta[];
 int mp[][];

 inline void init() {
     scanf("%d%d%d", &n, &m, &q);
 }

 int getSign(int x, int y) {
     top = ;
     sta[] = ;
     for(int i = ; i <= y; i++) {
         if(mp[x][i] > )
             sta[++top] = mp[x][i];
         else if(mp[x][i] < )
             top--;
     }
     return sta[top];
 }

 inline void solve() {
     int opt, x1, y1, x2, y2;
     while(q--) {
         scanf("%d%d%d%d%d", &opt, &x1, &y1, &x2, &y2);
         switch(opt) {
             case :
                 for(int i = x1; i <= x2; i++)
                     mp[i][y1] = q, mp[i][y2 + ] = -;
                 break;
             case :
                 for(int i = x1; i <= x2; i++)
                     mp[i][y1] = , mp[i][y2 + ] = ;
                 break;
             case :
                 top = ;
                 puts((getSign(x1, y1) == getSign(x2, y2)) ? ("Yes") : ("No"));
                 break;
         }
     }
 }

 int main() {
     init();
     solve();
     return ;
 }

The Untended Antiquity(Brute force)

Solution 2 随机化标号

　　思想仍然是差分，这次思考能不能想普通的差分一样做，可以扔进某个数据结构维护前缀和。

　　是不是可以前面 + 标号，右边的后一个 - 标号？很遗憾这么做是错误的。

　　比如一处+1 +2，而另一处是+3，显然它们不在一个平面内，但是这个算法会认为它们在一个平面内。

　　那怎么办呢？rand啊！没人知道它的标号是什么，可以通过两次rand得到一个30位的数，这样几乎不可能被卡掉。

Code

 /**
  * Codeforces
  * Problem#869E
  * Accepted
  * Time: 109ms
  * Memory: 49300k
  */
 #include <bits/stdc++.h>
 using namespace std;
 //#define lowbit(_x) (_x & (-_x))
 #define ll long long
 #define pii pair<int, int>

 int n, m, q;
 int top = ;
 ll f[][];
 map< pair< pii, pii >, int> g;

 inline int lowbit(int x) {
     return x & -x;
 }

 inline void init() {
     scanf("%d%d%d", &n, &m, &q);
 }

 inline int rd() {
     return rand() <<  | rand();
 } 

 inline void add(int x, int y, int val) {
     for(; x <= n + ; x += lowbit(x))
         for(int j = y; j <= m + ; j += lowbit(j))
             f[x][j] += val;
 }

 inline ll getSum(int x, int y) {
     ll rt = ;
     for(; x; x -= lowbit(x))
         for(int j = y; j; j -= lowbit(j))
             rt += f[x][j];
     return rt;
 }

 template<typename V, typename K>
 pair<V, K> makepair(V a, K b) {
     return pair<V, K>(a, b);
 }

 inline void solve() {
     srand((unsigned) time (NULL));
     for(int i = ; i <= ; i++)
         srand(rd());
     int opt, x1, y1, x2, y2, v;
     while(q--) {
         scanf("%d%d%d%d%d", &opt, &x1, &y1, &x2, &y2);
         switch(opt) {
             case :
                 v = rd();
                 g[makepair(pii(x1, y1), pii(x2, y2))] = v;
                 add(x2 + , y2 + , v), add(x1, y1, v);
                 add(x1, y2 + , -v), add(x2 + , y1, -v);
                 break;
             case :
                 v = g[makepair(pii(x1, y1), pii(x2, y2))];
                 add(x2 + , y2 + , -v), add(x1, y1, -v);
                 add(x1, y2 + , v), add(x2 + , y1, v);
                 break;
             case :
 //                cerr << getSum(x1, y1) << " " << getSum(x2, y2) << endl;
                 puts((getSum(x1, y1) == getSum(x2, y2)) ? ("Yes") : ("No"));
                 break;
         }
     }
 }

 int main() {
     init();
     solve();
     return ;
 }