linux的/etc/passwd、/etc/shadow、/etc/group和/etc/gshadow—关于用户和组的配置文件
获取数据:
内部数据和外部数据:内部数据比外部数据可靠
一手数据和二手数据:一手数据比二手数据可靠
抽样方法:
概率抽样,例如调查某大学学生跑1000米的成绩
- 简单随机抽样:去学校随机调查看到的学生
- 分层抽样:对大一、大二、大三、大四各选取一定数量的学生进行调查
- 整群抽样:不区分性别,需要对男生和女生都进行调查
- 系统抽样(等距抽样):按照一定规则对学号进行抽样,
非概率抽样,主要适用于所需调查的问题不具有普遍性,例如调查某大学学生每周阅读英文杂志的时长
- 方便抽样:研究者选取自己熟悉的人进行调查
- 判断抽样:研究者根据自己的判断决定是否对偶一个人进行调查
- 自愿抽样:被研究者自愿参与调查,自愿抽样在遇到敏感问题时往往会收到比较极端的结果
- 滚雪球抽样:选取到被调查者,被调查者再推荐满足条件的人参与调查
数据误差
- 抽样误差
- 非抽样误差:抽样框误差、回答误差、非回答误差、调查员误差等
Z score标准化
z=(x-μ)/σ,其中x为某一具体数,μ为平均数,σ为标准差
描述统计
集中趋势:平均数、中位数、众数
离散趋势:极值、四分位差
正态分布
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布,记为N(μ,σ^2),其概率密度函数为正态分布,期望值μ决定了其位置,标准差σ决定了分布的幅度。当μ = 0、σ = 1时的正态分布是标准正态分布,且 (X-μ)/σ 服从标准正态分布N(0,1)。
根据经验,距均值竖线左右两侧分别1个标准差的竖线,与正太曲线和横坐标轴围起来的面积约为整体面积的68%。
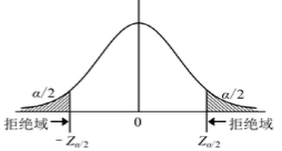
如果X1和X2为两个独立的满足正态分布的样本,则有如下结论。
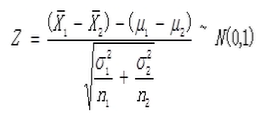
t分布
t-分布(t-distribution)用于根据小样本来估计呈正态分布且方差未知的总体的均值。t分布曲线形态与与自由度df有关,与标准正态分布曲线相比自由度df越小,t分布曲线愈平坦,中间愈低双侧尾部翘得愈高;自由度df愈大,t分布曲线愈接近正态分布曲线;当自由度df=∞时,t分布曲线为标准正态分布曲线,一般为30时从生成的图表上来看基本重合。
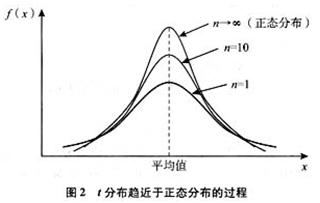

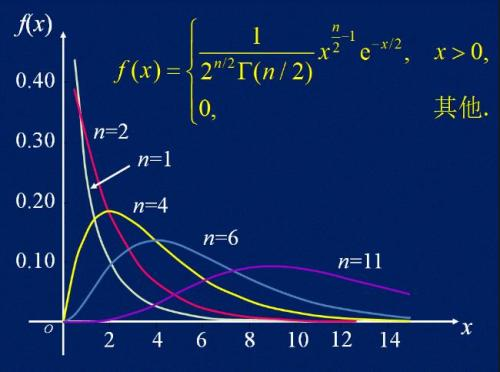
卡方分布
若n个相互独立的随机变量ξ₁,ξ₂,...,ξn服从标准正态分布(也称独立同分布于标准正态分布),则这n个随机变量的平方和构成一组新的随机变量,其分布规律称为卡方分布(chi-square distribution),ξ~x2(n)。由于平方过所以卡方分布的值不会小于0.
F分布
若总体X~N(0,1),(X1,X2,...,Xn1)与(Y1,Y2,...,Yn2)为来自X的两个独立样本,即x~x2(n1),y~x2(n2),设统计量F=(x/n1)/(y/n2),则统计量F服从自由度n1和n2的F 分布,记为F~F(n1,n2)

点估计和区间估计
区间估计为[样本均值-一定置信水平下置信度,样本均值+一定置信水平下置信度]
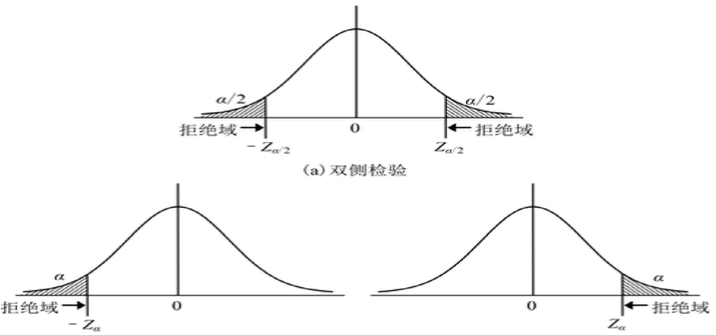
假设检验前提:总体符合正太分布
假设检验原理:
H0:μ=100
H1:μ≠100
对统计样本进行检验,如果P>显著性水平α→H0,P<显著性水平α→H0
单因素方差分析
假设检验原理:
H0:xx因素不影响因变量
H1:xx因素影响因变量
几个概念(xij表示样本值,x拔表示每组的样本均值,x拔拔表示所有样本均值,n表示样本数量,k表示组数,)
组内平方和 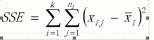
组内均方和 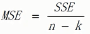
总平方和 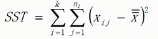
组间平方和 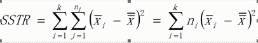
组间均方 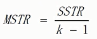
单因素方差分析F值计算 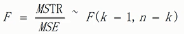
推导SST = SSE + SSTR,即总平方和=组内平方和+组间平方和
DFsst = DFSSE + DFSSTR
无交互因素双因素方差分析
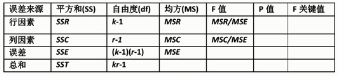
假设检验原理(2套):
H0:行因素不影响因变量(set1)
H1:行因素显著影响因变量(set1)
H0:列因素不影响因变量(set2)
H1:列因素显著影响因变量(set2)
双因素交互作用
假设检验原理:
H0:行因素和列因素互相独立,无交互作用
H1:行因素和列因素互相影响,有交互作用
线性回归
一元线性回归:一个自变量与因变量的线性关系,形如y = a + bx + e
多元线性回归:多个自变量与因变量的线性关系,形如y = a + b1x1 + b2x2 + ··· + bnxn + e
R square表示因变量有多少可以由自变量解释
对于多元线性回归,即使某一因素对因变量的解释能力很弱,但是如果将其加入模型R2仍然会增加,这就可能会出现虽然R2很高,但其实模型中有一些不太相关的自变量,为了解决这个问题引入了调整R square的概念,Ra2与R2的关系如下,随着R2的增大而增大,随着因变量个数的增加而减小。
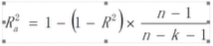
linux的/etc/passwd、/etc/shadow、/etc/group和/etc/gshadow—关于用户和组的配置文件的更多相关文章
- 文件/etc/passwd,/etc/shadow,/etc/group
文件/etc/passwd /etc/shadow /etc/group 计算资源的使用(并不是所有的人都可以用这台计算机的) 权限:访问资源的的能力. 用户:获取资源或者权限的凭证. 用户的容器:关 ...
- 【Linux命令】id,usermod用户管理命令(包括/etc/passwd、shadow、group、gshadow文件)
一.id命令 可以用来查看用户的UID.GID和附加组信息 id会显示用户以及所属群组的实际与有效ID.若两个ID相同,则仅显示实际ID.若仅指定用户名称,则显示目前用户的ID. 1.格式 id [O ...
- 关于Ubuntu中passwd、shadow、group等文件
在Ubuntu系统中,/etc目录下,有三个文件:passwd shadow group,可能我们已经在用了,但是没有注意到其详细. 这三个配置文件用于系统帐号管理,都是文本文件,可用vi等文本编辑器 ...
- 用户和用户组管理——passwd、shadow、group、gshadow
在Linux操作系统中,任何一个文件都归属于某一个特定的用户,而任何一个用户都归属于至少一个用户组. 1.用账号文件——passwd 该文件在/etc/passwd 目录下,是保证系统安全的关键文件. ...
- Linux中用户与组相关配置文件(整理)
用户与组信息存放位置 说明 注释 /etc/passwd 存放用户基本信息 记录了每个用户的一些基本属性,并对所有用户可读,每一行记录对应一个用户,属性之间通过冒号分隔. 每一个行6个冒号,7个属性. ...
- Linux用户和组的配置文件
用户和组的主要配置文件 前两个是放用户账号相关的,后两个是放和组相关的 /etc/passwd:用户及其属性信息(名称.UID.主组ID等) #早期密码也放这里,后来发现不安全,谁都能看 /etc/s ...
- passwd、shadow、group文件格式
[root@bogon ~]# cat /etc/passwd root:x:0:0:root:/root:/bin/bash 登录名:密码占位符:UID:GID:注释:家目录:用户的默认shell ...
- Linux下的用户、组和权限
目录 一:用户和组信息的查看 查看用户信息 查看密码信息 查看组信息 特殊组wheel 二:用户和组信息的管理 用户管理 组管理 三:文件权限 文件权限的查看 文件权限的修改 ACL控制权限 setf ...
- Linux 创建修改删除用户和组
200 ? "200px" : this.width)!important;} --> 介绍 在日常的维护过程中创建用户操作用的相对会多一些,但是在这个过程中涉及到的知识点就 ...
随机推荐
- fasttext学习笔记
When to use FastText? The main principle behind fastText is that the morphological structure of a wo ...
- Python 深浅copy 和文件操作
深浅copy 1,先看赋值运算. l1 = [1,2,3,['barry','alex']] l2 = l1 l1[0] = 111 print(l1) # [111, 2, 3, ['barry', ...
- log4j.properties配置详解与实例-全部测试通过[转]
最近使用log4j写log时候发现网上的写的都是千篇一律,写的好的嘛不全,写的全一点的嘛没有一点格式,看着累.这里把网上收集到的整理了一下,并且全部都在机器上测试成功了.这么好的文档估计没有了吧? # ...
- Http 服务 简单示例
现在我们实现一个GO的Web http服务 只做演示,没有实际功能 但是能看出Go做Http服务的简洁 **************************************** package ...
- node.js之爬虫
nodejs爬取数据出现编码错误的问题 可以使用 superagent-charset 和 superagent 模块进行处理 var charset = require('superagent-ch ...
- selenium获取文本
# 标题list_title = driver.find_elements_by_xpath('//*[@id="share-content"]/div/div[1]/ul/li/ ...
- Android -- 仿淘宝广告条滚动
1,在赶项目的时候我们经常会实现下面这个功能,及添加滚动条广告广播,先看一下淘宝的效果 2,这次实现效果主要使用Android自带的ViewFlipper控件,先来看一下我们的它的基本属性和基本方法吧 ...
- CRUD简单查询
一.查询所有数据 select * from car 二.查询指定列 select code , price from car 三.修改查询出的列名 select code as '代号' , nam ...
- Oracle使用rman备份数据库时出现cannot reclaim的错误
1. 按照<2 day DBA>中的guide,设置fast recovery area. SQL> ALTER SYSTEM SET DB_RECOVERY_FILE_DEST_S ...
- HashMap集合存储自定义类
第一种情况,key为String,value为自定义类person类: 输出结果,key重复的被去掉了,key重复的那个value值之前的被最后一个覆盖了: 第二种情况,key为自定义类person类 ...
