1、设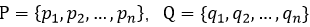是两组Rd空间的点集，可根据这两个点集计算它们之间的旋转平移信息。

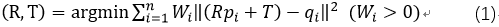
2、设R为不变量，对T求导得：

令

则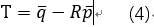

将(4)带入(1)得：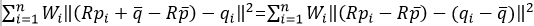

令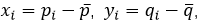

则

(相当于对原来点集做减中心点预处理，再求旋转量)

3、 计算旋转量

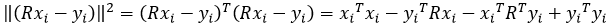
因为R为正交阵且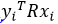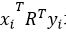，均为标量，

所以

所以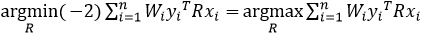

而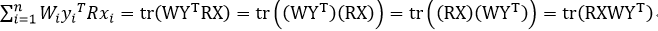

令，对S进行SVD分解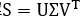，则

令，则M为正交阵，

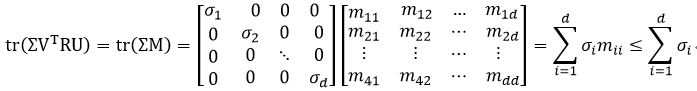
要求得最大迹，则使mii=1,则M必为单位阵，即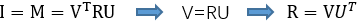

SVD分解求解旋转矩阵的更多相关文章

  1. SVD分解技术详解

    版权声明: 本文由LeftNotEasy发布于http://leftnoteasy.cnblogs.com, 本文可以被全部的转载或者部分使用,但请注明出处,如果有问题,请联系wheeleast@gm ...

  2. SVD分解　解齐次线性方程组

    SVD分解 只有非方阵才能进行奇异值分解 SVD分解:把矩阵分解为 特征向量矩阵+缩放矩阵+旋转矩阵 定义 设\(A∈R^{m×n}\),且$ rank(A) = r (r > 0) $,则矩阵 ...

  3. 机器学习之SVD分解

    一.SVD奇异值分解的定义 假设是一个的矩阵,如果存在一个分解: 其中为的酉矩阵,为的半正定对角矩阵,为的共轭转置矩阵,且为的酉矩阵.这样的分解称为的奇异值分解,对角线上的元素称为奇异值,称为左奇异矩 ...

  4. 矩阵的SVD分解

    转自 http://blog.csdn.net/zhongkejingwang/article/details/43053513(实在受不了CSDN的广告) 在网上看到有很多文章介绍SVD的,讲的也都 ...

  5. SVD分解及线性最小二乘问题

    这部分矩阵运算的知识是三维重建的数据基础. 矩阵分解 求解线性方程组:,其解可以表示为. 为了提高运算速度,节约存储空间,通常会采用矩阵分解的方案,常见的矩阵分解有LU分解.QR分解.Cholesky ...

  6. 机器学习Python实现 SVD 分解

    这篇文章主要是结合机器学习实战将推荐算法和SVD进行对应的结合 不论什么一个矩阵都能够分解为SVD的形式 事实上SVD意义就是利用特征空间的转换进行数据的映射,后面将专门介绍SVD的基础概念.先给出p ...

  7. SVD分解

    首先,有y = AX,将A看作是对X的线性变换 但是,如果有AX = λX,也就是,A对X的线性变换,就是令X的长度为原来的λ倍数. *说起线性变换,A肯定要是方阵,而且各列线性无关.(回想一下,A各 ...

  8. SVD分解的理解[转载]

    http://www.bfcat.com/index.php/2012/03/svd-tutorial/ SVD分解(奇异值分解),本应是本科生就掌握的方法,然而却经常被忽视.实际上,SVD分解不但很 ...

  9. 机器学习中的矩阵方法04：SVD 分解

    前面我们讲了 QR 分解有一些优良的特性,但是 QR 分解仅仅是对矩阵的行进行操作(左乘一个酉矩阵),可以得到列空间.这一小节的 SVD 分解则是将行与列同等看待,既左乘酉矩阵,又右乘酉矩阵,可以得出 ...

随机推荐

  1. mysql 如何在访问某张数据表按照某个字段分类输出

    也许大家有时候会遇到需要将把数据库中的某张表的数据按照该表的某个字段分类输出,比如一张数据表area如下 我们需要将里面的area按照serialize字段进行分类输出,比如这种形式: areas   ...

  2. 【阅读笔记】《C程序员 从校园到职场》第二章 学校到职场

    一.代码规范: 1.变量命名(让人一眼看它是什么意思,要做什么操作),定义并初始化 2.函数命名规范(函数的功能)在主函数之前进行声明. 在实际项目中,一般不在函数调用者的内部来对被调函数进行声明,而 ...

  3. 使用RxSwift 实现登录页面的条件绑定

    我们在使用MVC建构进行开发时,对登录页面用户名密码等进行的处理一般是这样的,点击登录按钮判断用户框以及密码框输入的合法性,用一堆if真是屎一般!或者用textfield的代理来进行响应其实也是屎一般 ...

  4. 软件设计基础-C/S系统

    在软件设计开发过程中,逐渐形成了一些针对特定应用领域的软件系统组织方式的惯用模式 如经典的C/S(client/server,客户/服务器)模式和B/S(browser/server,浏览器/服务器) ...

  5. 第三篇 功能实现(1) (Android学习笔记)

    第三篇 功能实现(1) 第8章 Android应用程序组成 ●Android的一些中.底层基础知识 ※ Android Framework 启动过程 Android手机系统本质上是一个基于Linux的 ...

  6. ：策略模式--Duck

    原则:封装变化的部分:针对超类编程,不针对实现:多组合少继承: #ifndef __DUCK_H__ #define __DUCK_H__ #include "FlyBehavior.h&q ...

  7. ６.3 C++修改字符串

    参考:http://www.weixueyuan.net/view/6392.html 总结: string字符串同样可以像字符串数组那样按照下标逐一访问字符串中的每一个字符,string字符串的起始 ...

  8. Linux关闭防火墙步骤

    1   先查询防火墙状态 [root@old-09 ~]# /etc/init.d/iptables status Table: filter Chain INPUT (policy ACCEPT) ...

  9. nio的简单学习

    参考链接: http://www.iteye.com/magazines/132-Java-NIO https://www.cnblogs.com/xiaoxi/p/6576588.html http ...

  10. 禁止textarea拉伸

    添加css属性: style="resize:none" ;