HDU 5950 - Recursive sequence - [矩阵快速幂加速递推][2016ACM/ICPC亚洲区沈阳站 Problem C]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=5950

Farmer John likes to play mathematics games with his N cows. Recently, they are attracted by recursive sequences. In each turn, the cows would stand in a line, while John writes two positive numbers a and b on a blackboard. And then, the cows would say their identity number one by one. The first cow says the first number a and the second says the second number b. After that, the i-th cow says the sum of twice the (i-2)-th number, the (i-1)-th number, and $i^4$. Now, you need to write a program to calculate the number of the N-th cow in order to check if John’s cows can make it right.

Input
The first line of input contains an integer t, the number of test cases. t test cases follow. 
Each case contains only one line with three numbers N, a and b where $N,a,b < 2^31$ as described above.

Output
For each test case, output the number of the N-th cow. This number might be very large, so you need to output it modulo $2147493647$.

Sample Input
2
3 1 2
4 1 10

Sample Output
85
369

Hint
In the first case, the third number is $85 = 2 \times 1 + 2 + 3^4$.
In the second case, the third number is $93 = 2 \times 1 + 1 \times 10 + 3^4$ and the fourth number is $369 = 2 \times 10 + 93 + 4^4$.

题意：

给出 $a,b,n$，已知 $a_1 = a, a_2 = b$，且对于 $i>2$ 的 $a_i = 2a_{i-2} + a_{i-1} + i^4$，求 $a_n$。

题解：

看一眼 $n$ 最大在 $2e9$，显然不是暴力的递推。考虑矩阵快速幂加速递推。

不妨设一个矩阵

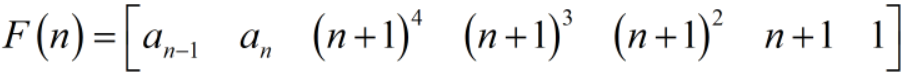
那么就有

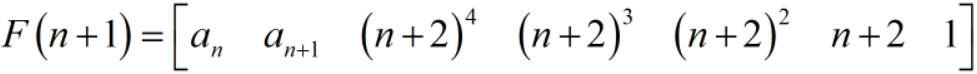
我们只要求出一个矩阵 $A$，使其满足 $F(n+1) = F(n) \times A$，就能进行矩阵快速幂加速递推。

根据二项式定理很容易得到

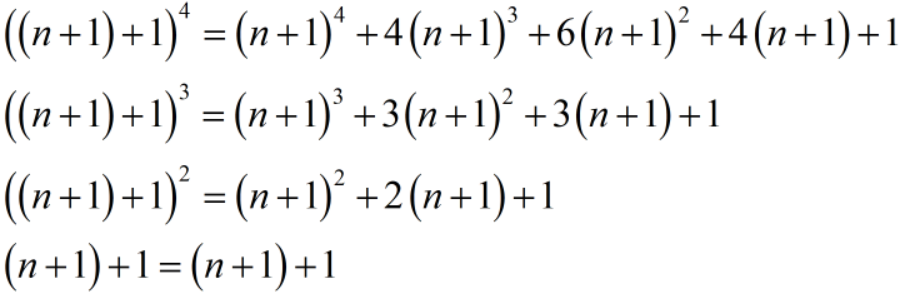
因此不难就求得满足 $F(n+1) = F(n) \times A$ 矩阵 $A$ 如下：

此时，对于任意的 $F(n)$，都可以由 $F(n) = F(2) \times A^{n-2}$ 求得，$A^{n-2}$ 用矩阵快速幂可以 $O(\log n)$ 求出。

AC代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=;

const int DIM=;
struct Matrix
{
    ll mat[DIM][DIM];
    Matrix operator*(Matrix const &oth)const
    {
        Matrix res;
        memset(res.mat,,sizeof(res.mat));
        for(int i=;i<DIM;i++)
            for(int j=;j<DIM;j++)
                for(int k=;k<DIM;k++)
                    res.mat[i][j]+=(mat[i][k]*oth.mat[k][j])%mod,
                    res.mat[i][j]%=mod;
        return res;
    }
}A,F2,Fn;
Matrix fpow(Matrix base,ll n)
{
    Matrix res;
    memset(res.mat,,sizeof(res.mat));
    for(int i=;i<DIM;i++) res.mat[i][i]=;
    while(n)
    {
        if(n&) res=res*base;
        base=base*base;
        n>>=;
    }
    return res;
}

void initA()
{
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
    A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=, A.mat[][]=;
}

ll n,a,b;
int main()
{
    ios::sync_with_stdio();
    cin.tie();

    initA();
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>a>>b;
        if(n==) {
            cout<<a<<'\n';
            continue;
        }
        if(n==) {
            cout<<b<<'\n';
            continue;
        }

        memset(F2.mat,,sizeof(F2.mat));
        memset(Fn.mat,,sizeof(Fn.mat));

        F2.mat[][]=a, F2.mat[][]=b,
        F2.mat[][]=***, F2.mat[][]=**, F2.mat[][]=*, F2.mat[][]=, F2.mat[][]=;

        Fn=F2*fpow(A,n-);
        cout<<Fn.mat[][]<<'\n';
    }
}