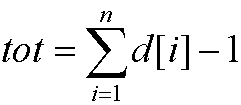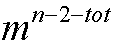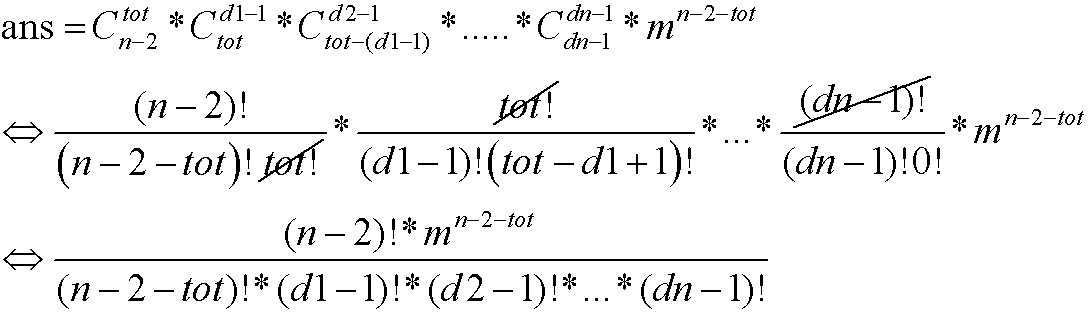BZOJ 1005 明明的烦恼 (组合数学)
题解:n为树的节点数,d[ ]为各节点的度数,m为无限制度数的节点数。
则
所以要求在n-2大小的数组中插入tot各序号,共有种插法;
在tot各序号排列中,插第一个节点的方法有种插法;
插第二个节点的方法有种插法;
.........另外还有m各节点无度数限制,所以它们可任意排列在剩余的n-2-tot的空间中,排列方法总数为
根据乘法原理:
#include <cstdio>
#include <cmath>
int n,m,tot,i,j,d,down[1005],up[1005],p[1005],ans[10005];
void pi(int x,int a[]){
for(int i=2;i<=x;i++)if(p[i]){
int sum=i; while(sum<=x)a[i]+=x/sum,sum*=i;
}
}
int main(){
scanf("%d",&n);
for(i=2;i<=1000;i++){
for(j=2;j<=std::sqrt(i);j++)
if(i%j==0)break;
if(j>sqrt(i))p[i]=1;
}
for(i=1;i<=n;i++){
scanf("%d",&d);
if(d==-1){m++;continue;}
if(d>1)pi(d-1,down);
tot+=d-1;
}
pi(n-2-tot,down);pi(n-2,up);
for(i=1;i<=1000;i++)up[i]-=down[i];
ans[0]=1;
for(i=1;i<=1000;i++)while(up[i]--){
for(j=0;j<=10000;j++)ans[j]*=i;
for(j=0;j<=10000;j++)if(ans[j]>9)ans[j+1]+=ans[j]/10,ans[j]%=10;
}
if(m)for(i=1;i<=n-2-tot;i++){
for(j=0;j<=10000;j++)ans[j]*=m;
for(j=0;j<=10000;j++)if(ans[j]>9)ans[j+1]+=ans[j]/10,ans[j]%=10;
}
if(tot>n-2||tot<n-2&&m==0)return puts("0"),0;
i=10000; while(!ans[i])i--;
while(~i)printf("%d",ans[i--]);
return 0;
}
BZOJ 1005 明明的烦恼 (组合数学)的更多相关文章
- [HNOI2008][bzoj 1005]明明的烦恼(prufer序列)
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 7121 Solved: 2816[Submit][Stat ...
- BZOJ 1005 明明的烦恼 Prufer序列+组合数学+高精度
题目大意:给定一棵n个节点的树的节点的度数.当中一些度数无限制,求能够生成多少种树 Prufer序列 把一棵树进行下面操作: 1.找到编号最小的叶节点.删除这个节点,然后与这个叶节点相连的点计入序列 ...
- [BZOJ]1005 明明的烦恼(HNOI2008)
BZOJ的第一页果然还是很多裸题啊,小C陆续划水屯些板子. Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间 ...
- BZOJ 1005 明明的烦恼
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为 ...
- BZOJ 1005 明明的烦恼(prufer序列+高精度)
有一种东西叫树的prufer序列,一个树的与一个prufer序列是一一对应的关系. 设有m个度数确定的点,这些点的度为dee[i],那么每个点在prufer序列中出现了dee[i]-1次. 由排列组合 ...
- BZOJ 1005: [HNOI2008]明明的烦恼( 组合数学 + 高精度 )
首先要知道一种prufer数列的东西...一个prufer数列和一颗树对应..然后树上一个点的度数-1是这个点在prufer数列中出现次数..这样就转成一个排列组合的问题了.算个可重集的排列数和组合数 ...
- BZOJ1005:[HNOI2008]明明的烦恼(组合数学,Prufer)
Description 自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为N ...
- BZOJ 1005 [HNOI2008] 明明的烦恼(组合数学 Purfer Sequence)
题目大意 自从明明学了树的结构,就对奇怪的树产生了兴趣...... 给出标号为 1 到 N 的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树? Input 第一行为 N( ...
- BZOJ 1005 [HNOI2008]明明的烦恼 (Prufer编码 + 组合数学 + 高精度)
1005: [HNOI2008]明明的烦恼 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 5786 Solved: 2263[Submit][Stat ...
随机推荐
- hadoop搭建杂记:Linux下JDK环境变量的设置(三种配置环境变量的方法)
Linux下JDK环境变量的设置(三种配置环境变量的方法) Linux下JDK环境变量的设置(三种配置环境变量的方法) ①修改/etc/profile文件 如果你的计算机仅仅作为开发使用时推荐使用这种 ...
- 本地搭建php环境
AppServ 是 PHP 网页架站工具组合包,所包含的软件有:Apache[.Apache Monitor.PHP.MySQL.phpMyAdmin等,如果您的本地机器没有安装过php.mysql等 ...
- 原生js动态改变dom高度
item参数为要改变高度的dom,maxHight参数为dom的最大高度,speed参数为改变高度的速度function addHeight(item,maxHight,speed){ var ite ...
- Python3 关于UnicodeDecodeError/UnicodeEncodeError: ‘gbk’ codec can’t decode/encode bytes类似的文本编码问题
以下是小白的爬虫学习历程中遇到并解决的一些困难,希望写出来给后来人,如有疏漏恳请大牛指正,不胜感谢! 首先,我的代码是这样的 import requests url = 'http://www.acf ...
- if最简单的用法
/* Name:if最简单的用法-1 Copyright:By.不懂网络 Author: Yangbin Date:2014年2月9日 03:00:58 Description:if最简单的用法,真则 ...
- RTTI-CLASS
package com.xt.test; interface Test1Interface { } interface Test2Interface { } class Test1 implement ...
- Openstack命令收集
查看rabbitmq 队列 rabbitmqctl list_queues 查看keystone的用户 keystone user-list 查看keystone endpoint keystone ...
- Using SetWindowRgn
Using SetWindowRgn Home Back To Tips Page Introduction There are lots of interesting reasons for cre ...
- kbengine简单介绍(1)
什么是kbengine? 一款开源的游戏服务端引擎,客户端通过简单的约定协议就能与服务端通讯, 使用KBEngine插件能够快速与(Unity3D, OGRE, Cocos2d-x, HTML5, 等 ...
- poj 2406 Power Strings(KMP变形)
Power Strings Time Limit: 3000MS Memory Limit: 65536K Total Submissions: 28102 Accepted: 11755 D ...