算法精解（C语言描述） 第3章 读书笔记

第3章 递归

1、基本递归

假设想计算整数n的阶乘，比如4！=4×3×2×1。

迭代法：循环遍历其中的每一个数，然后与它之前的数相乘作为结果再参与下一次计算。可正式定义为：n! = (n)(n-1)(n-2)…(1)。

递归法：将n!定义为更小的阶乘形式。可以正式定义为：

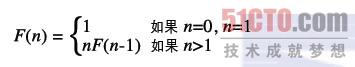
递归过程中的两个基本阶段：递推与回归。

递推阶段，每一个递归调用通过进一步调用自己来记住这次递归过程。当其中有调用满足终止条件时，递推结束。每一个递归函数都必须拥有至少一个终止条件；否则，递推阶段就永远不会结束了。一旦递推阶段结束，处理过程就进入回归阶段，在这之前的函数调用以逆序的方式回归，直到最初调用的函数返回为止，此时递归过程结束。

 示例3-1：以递归方式计算阶乘的函数实现

/* fact.c */
#include "fact.h"
/* fact */
int fact(int n) {
if (n < )
   return ;
else if (n == )
   return ;
else if (n == )
   return ;
else
   return n * fact(n - );
} 

补充知识点 ： C程序在内存中的组织方式

基本上来说一个可执行程序由4个区域组成：代码段、静态数据区、堆与栈（见图3-2a）。

　　1）代码段：包含程序运行时所执行的机器指令；

　　2）静态数据区：包含在程序生命周期内一直持久的数据，如全局变量和静态局部变量；

　　3）堆：包含程序运行时动态分配的存储空间，比如用malloc分配的内存；

　　4）栈：包含函数调用的信息。

按照惯例，堆的增长方向为从程序低地址到高地址向上增长，而栈的增长方向刚好相反（实际情况可能不是这样，与CPU的体系结构有关）。

注意：此处的堆与数据结构中的堆没有什么关系。

图3-2：a）C程序在内存中的组织形式  b）一份活跃记录

当C程序中调用了一个函数时，栈中会分配一块空间来保存与这个调用相关的信息。每一个调用都被当做是活跃的。栈上的那块存储空间称为活跃记录，或者称为栈帧。

栈帧由5个区域组成（见图3-2b）：

　　1）输入参数：传递到活跃记录中的参数

　　2）返回值空间：

　　3）计算表达式时用到的临时存储空间：

　　4）函数调用时保存的状态信息：

　　5）输出参数：传递给在活跃记录中调用的函数所使用的参数。

一个活跃记录中的输出参数就成为栈中下一个活跃记录的输入参数。函数调用产生的活跃记录将一直存在于栈中直到这个函数调用结束。

回到示例3-1，考虑一下当计算4!时栈中都发生了些什么。

初始调用fact会在栈中产生一个活跃记录，输入参数n=4（见图3-3，第1步）。

由于这个调用没有满足函数的终止条件，因此fact将继续以n=3为参数递归调用。这将在栈上创建另一个活跃记录，但这次输入参数（见图3-3，第2步）。这里，n=3也是第一个活跃期中的输出参数，因为正是在第一个活跃期内调用fact产生了第二个活跃期。

这个过程将一直继续，直到n的值变为1，此时满足终止条件，fact将返回1（见图3-3，第4步）。

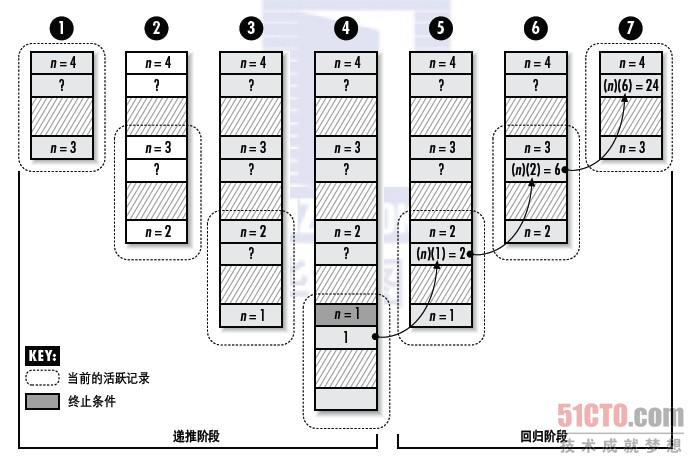
图3-3：递归计算4!时的C程序的栈

栈是用来存储函数调用信息的绝好方案，这归功于其后进先出的特点满足了函数调用和返回的顺序。然而，使用栈也有一些缺点。

　　1）栈维护了每个函数调用的信息直到函数返回后才释放，占用空间大，尤其是在程序中递归调用很多的情况下。

　　2）因有大量的信息需保存和恢复，故生成和销毁活跃记录需要耗费一定的时间。

解决方法：可以采用一种称为尾递归的特殊递归方式来避免前面提到的这些缺点。

2、尾递归

若一个函数中所有递归形式的调用都出现在函数的末尾，则称该递归函数是尾递归的。

当递归调用是整个函数体中最后执行的语句，且它的返回值不属于表达式的一部分时，该递归调用就是尾递归。

尾递归函数的特点是：在回归过程中不用做任何操作，大多数现代的编译器会利用该特点自动生成优化的代码。

当编译器检测到一个函数调用是尾递归时，它就覆盖当前的活跃记录，而不是在栈中去创建一个新的，从而将所使用的栈空间大大缩减，这使得实际的运行效率会变得更高。因此，只要有可能我们就需要将递归函数写成尾递归的形式。

之前对计算n!的定义：在每个活跃期计算n倍的(n－1)!的值，让n=n－1并持续这个过程直到n=1为止。这种定义不是尾递归的，因为每个活跃期的返回值都依赖于用n乘以下一个活跃期的返回值，因此每次调用产生的栈帧将不得不保存在栈上直到下一个子调用的返回值确定。

以尾递归的形式来定义计算n!的过程，函数可定义为以下形式：

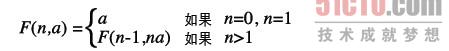
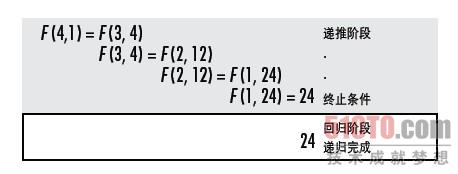
图3-4说明了用尾递归计算4!的过程。

注意在回归的过程中不需要做任何操作，这是所有尾递归函数的标志。

图3-4：以尾递归的方式计算4!

示例3-2：以尾递归的形式计算阶乘的一个函数实现

/* facttail.c */
#include "facttail.h"
/* facttail  */
int facttail(int n, int a) {
/* Compute a factorial in a tail-recursive manner. */
if (n < )
   return ;
else if (n == )
   return ;
else if (n == )
   return a;
else
   return facttail(n - , n * a);
}

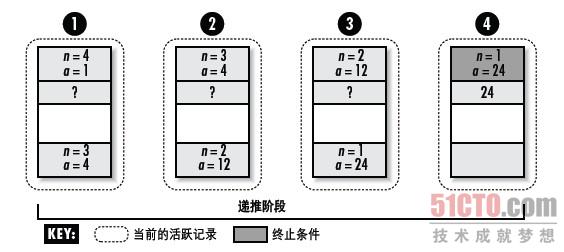
图3-5：以尾递归形式计算4!时栈的情况

3、问与答

问：以下递归定义中有错误，请指正。归并排序将一组数据一分为二，然后分别将两份数据各自再进行分半处理，一直持续这个过程直到每一份都只含一个元素。然后在回归过程中完成各份数据的合并最终产生一个有序的集合。

答：该定义的问题在于当n的初始值大于0时将永远无法满足终止条件n=0。为了解决问题，需要一个满足要求的终止条件。n－1这个条件就能很好满足，这意味着也要修改函数中的第二个条件。合适的递归定义应该是这样的：

问：以递归的思想描述一种求解整数质因子的方法。分析该方法是否是尾递归的并解释原因。

答：递归是一种求解整数质因子的很自然的方法，因为因子分解无非就是不断地解决同样的问题。每当确定了一个因子，剩余因子的集合就变得越来越小。针对这个问题的递归方法可以定义为如下式子：

这个定义的意思是说：为了递归地确定整数n的质因子，先确定它的最小质因子i并把它记录到集合P中，然后对整数n=n/i重复这个过程直到n本身成为质数为止，这就是终止条件。这个定义是尾递归的，因为在回归过程中不需要做任何处理，如图3-6所示。

图3-6：以尾递归的方式计算整数2409的质因子

问：思考当执行递归函数时栈的使用情况，当递归过程的递推阶段永远不会终止时会出现什么情况？

答：如果递归函数的终止条件永远得不到满足，最终栈的增长会超过可接受的值，程序会因为栈溢出而终止运行。当程序执行时，一个称为帧指针的特殊指针会寻址栈顶的帧。正是栈指针指向实际的栈顶（即，下一个栈帧将被压入的位置。因此，虽然某个系统可能使用来判断栈溢出，但是它可能是通常会使用的栈指针。）