[leetcode]239. Sliding Window Maximum滑动窗口最大值

Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return the max sliding window.

Example:

Input: nums = [1,3,-1,-3,5,3,6,7], and k = 3
Output: [3,3,5,5,6,7]
Explanation: 

Window position                Max
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

题意：

给定一个长度为k的滑动窗口不断从左往右滑动，给出过程中的各个最大值。

思路：

使用一个每次能取出极值的数据结构，TreeMap，如下图，其底层用BST来储存

TreeMap要求key必须是比较大小（自然排序或定制排序）

以[1,1,-1,-3,5,3,6,7], k = 3 为例， 遍历数组，将数组每个元素作为TreeMap的key, 将该元素出现频率作为对应value

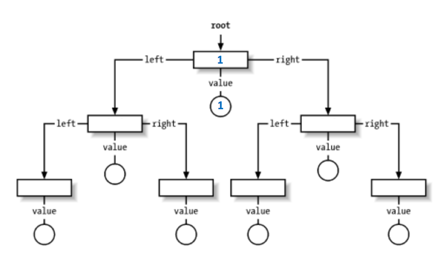
[1,　　1,　　 -1,　　 -3,　　5,　　3,　　6,　　7]

^ i = 0

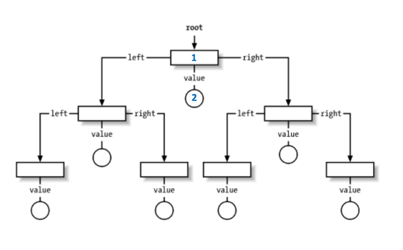
[1,　　1,　　 -1,　　 -3,　　5,　　3,　　6,　　7]

^ i = 1

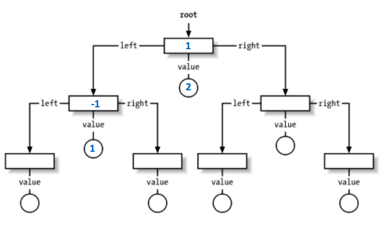
[1,　　1,　　 -1,　　 -3,　　5,　　3,　　6,　　7]

^   i = 2

[1,　　1,　　 -1,　　 -3,　　5,　　3,　　6,　　7]

^  i = 3 此时 i >= k  则先将a[i-k]在TreeMap中对应的出现频率(value) 减1

再check一下 a[i-k]对应的value是否为0，为0则直接删去。

此例中，a[i-k] = 1， 在TreeMap中对应的value为2，那么value减1 后为1， 仍然继续保留。

由此可以看出，大体思路是用TreeMap维护一个所有value值相加为K的BST

用lastKey()来取出当前TreeMap里最大值(根据BST性质，最大值一定在最右）

代码：

 class Solution {
     public int[] maxSlidingWindow(int[] a, int k) {
         // corner case
         if(k <= 0) return new int[]{};
         //TreeMap要求其key必须可比较大小
         TreeMap<Integer, Integer> map = new TreeMap<>((o1,o2) -> o1 - o2);
         int[] result = new int[a.length - k + 1];

         for(int i = 0; i < a.length; i++){
             // 1. add to bst
             if(map.containsKey(a[i])){
                 map.put(a[i], map.get(a[i]) + 1 );
             }else{
                 map.put(a[i], 1);
             }
             // 2. remove from bst when window sliding
             if( i >= k){
                 map.put(a[i - k] , map.get(a[i - k]) - 1 );
                 if(map.get(a[i - k]) == 0 ){
                     map.remove(a[i - k]);
                 }
             }
             // 3. get max
             if( i + 1 >= k){
                 result[ i - (k - 1)] = map.lastKey();
             }
         }
         return result;
     }