洛谷 P4128 [SHOI2006]有色图 解题报告

P4128 [SHOI2006]有色图

题目描述

如果一张无向完全图（完全图就是任意两个不同的顶点之间有且仅有一条边相连）的每条边都被染成了一种颜色，我们就称这种图为有色图。如果两张有色图有相同数量的顶点，而且经过某种顶点编号的重排，能够使得两张图对应的边的颜色是一样的，我们就称这两张有色图是同构的。以下两张图就是同构的，因为假如你把第一张图的顶点\((1,2,3,4)\)置换成第二张图的\((4,3,2,1)\)，就会发现它们是一样的。

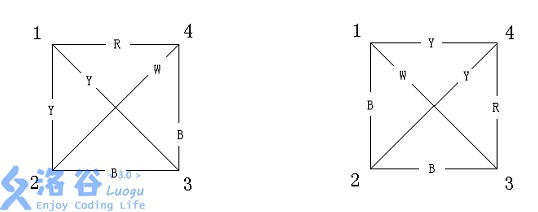
你的任务是，对于计算所有顶点数为\(n\)，颜色种类不超过\(m\)的图，最多有几张是两两不同构的图。由于最后的答案会很大，你只要输出结论模\(p\)的余数就可以了（\(p\)是一个质数）

输入输出格式

输入格式：

输入文件只有一行，由三个正整数\(n,m,p\)组成，他们满足\(1≤n≤53\)，\(1≤m≤1000\)，\(n＜p≤10^9\)

输出格式：

即总数模\(p\)后的余数

---

我们发现\(polya\)处理的是点的置换，现在要处理边的，怎么办呢？

其实是一样的，我们发现每个点的置换都可以对应一个边的置换，边的置换同样构成了一个群，注意这个群的大小和点的置换组成的群的大小是一样的。

然后我们枚举本质不同的点的置换，这个本质不同是按轮换大小的集合定义的，相当于对\(n\)进行和式拆分，相当于\(n=L_1+L_2+\dots+L_p\)，\(L\)是每个轮换的大小，这个状态量是比较小的。

注意搜的时候为了避免重复，需要\(L_1\le L_2\le \dots L_p\)这样搜

这时候就可以通过点的置换求出边的置换的轮换大小的信息了。

分类讨论

• 当两个点处于两个不同轮换\(L_i\)和\(L_j\)中时，产生的边的轮换的大小为$\frac{L_i,L_j}{lcm(L_i,L_j)}=\gcd(i,j) $，就是考虑两个点一起转，然后要转公倍数那么长才回来
• 当两个点处于同一轮换\(L_i\)中时
  • 当\(L_i\)为奇数，轮换个数为\(\frac{L_i*(L_i-1)}{2*L_i}=\frac{L_i-1}{2}\)，每个轮换长度为\(L_i\)
  • 当\(L_i\)为偶数，轮换个数为\(\frac{\frac{L_i(L_i-1)}{2}-\frac{L_i}{2}}{L}+1=\frac{L_i}{2}\)，这里有一个轮换长度为\(\frac{L_i}{2}\)，是相差长度等于\(\frac{L_2}{2}\)的点组成的边所在的集合。

然后统计所有轮换的贡献\(C=\sum\lfloor\frac{L_1}{2}\rfloor+\sum\sum \gcd(L_i,L_j)\)

再统计一下枚举的\(L\)的总情况，为\(D=\frac{n!}{\prod_{i=1}^pL_i\prod_{i=1}^kB_i}\)，其中\(B_i\)为\(\sum_{j=1}^p[L_j=i]\)，这点除\(L_i\)是每种情况都是一个圆排列，除\(B_i\)是每个同样大小的圆排列是无标号的。

答案是\(\frac{\sum Dm^C}{n!}\)

---

#include <cstdio>
int ans,L[60],fac[60],n,m,mod,cnt;
#define mul(a,b) (1ll*(a)*(b)%mod)
#define add(a,b) ((a+b)%mod)
int gcd(int a,int b){return b?gcd(b,a%b):a;}
int qp(int d,int k){int f=1;while(k){if(k&1)f=mul(f,d);d=mul(d,d),k>>=1;}return f;}
void cal()
{
    int C=0,S=1;
    for(int i=1;i<=cnt;i++)
        C=add(C,L[i]/2);
    for(int i=1;i<=cnt;i++)
        for(int j=i+1;j<=cnt;j++)
            C=add(C,gcd(L[i],L[j]));
    int B=1;
    for(int i=1;i<=cnt;i++)
    {
        if(L[i]!=L[i-1])
        {
            S=mul(S,fac[B]);
            B=0;
        }
        ++B;
        S=mul(S,L[i]);
    }
    S=mul(S,fac[B]);
    S=qp(S,mod-2);
    C=qp(m,C);
    ans=add(ans,mul(S,C));
}
void dfs(int res,int lim)
{
    if(!res) cal();
    for(int i=lim;i<=res;i++)
    {
        L[++cnt]=i;
        dfs(res-i,i);
        --cnt;
    }
}
int main()
{
    scanf("%d%d%d",&n,&m,&mod);
    fac[0]=1;
    for(int i=1;i<=n;i++) fac[i]=mul(fac[i-1],i);
    dfs(n,1);
    printf("%d\n",ans);
    return 0;
}

---

2018.12.22